题目内容
20.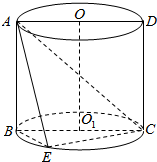 如图:已知矩形ABCD是圆柱OO1的轴截面,E是下底面圆周上的一点.
如图:已知矩形ABCD是圆柱OO1的轴截面,E是下底面圆周上的一点.(1)求证:平面ABE⊥平面AEC;
(2)若三棱锥A-BEC的体积与圆柱体OO1的体积之比为1:6π时.求∠BCE的大小.
分析 (1)证明EC⊥平面ABE,即可证明平面ABE⊥平面AEC;
(2)求出三棱锥A-BEC的体积与圆柱体OO1的体积,利用比为1:6π,求∠BCE的大小.
解答 (1)证明:∵BC是直径,
∴EC⊥BE,
∵EC⊥AB,AB∩BE=B,
∴EC⊥平面ABE,
∵EC?平面AEC,
∴平面ABE⊥平面AEC;
(2)解设BC=2R,∠BCE=α
∵三棱锥A-BEC的体积与圆柱体OO1的体积之比为1:6π,
∴$\frac{1}{3}×\frac{1}{2}×BCsinα×BCcosα×AB$:(π×BC2×AB)=1:6π,
∴sin2α=$\frac{1}{2}$,
∴α=$\frac{π}{12}$.
点评 本题考查平面与平面垂直的证明,考查体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.设集合A={x|1<x<4},集合B={x|-1≤x≤3},则A∩(∁RB)等于( )
| A. | (1,4) | B. | (3,4) | C. | (1,3) | D. | (1,2)∪(3,4) |
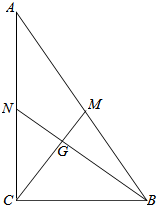 如图,在Rt△ABC中,∠BCA=90°.CM与BN相交于点G,且CM⊥BN.若G是△ABC的重心,BC=2.求BN的长.
如图,在Rt△ABC中,∠BCA=90°.CM与BN相交于点G,且CM⊥BN.若G是△ABC的重心,BC=2.求BN的长.