Question

5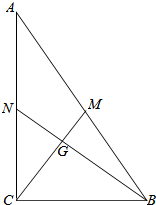．如图，在Rt△ABC中，∠BCA=90°．CM与BN相交于点G，且CM⊥BN．若G是△ABC的重心，BC=2．求BN的长．

Answer 1

分析 设CN=x，根据重心的性质和勾股定理，构造关于x的方程，解方程求出x的值，进而可得BN的长．

解答 解：∵在Rt△ABC中，BC=2，G是△ABC的重心且∠BCA=90°，
∴M，N分别为AB，AC边的中点，
设CN=x，则AC=2x，
在Rt△ABC中，AB=$\sqrt{4+4{x}^{2}}$=2$\sqrt{1+{x}^{2}}$，
∴CM=$\frac{1}{2}$AB=$\sqrt{1+{x}^{2}}$，
∴CG=$\frac{2}{3}$CM=$\frac{2}{3}$$\sqrt{1+{x}^{2}}$，
在Rt△NBC中，BN=$\sqrt{4+{x}^{2}}$，
∴BG=$\frac{2}{3}$BN=$\frac{2}{3}$$\sqrt{4+{x}^{2}}$，
又∵CM⊥BN．
∴在Rt△GBC中，BG²+CG²=BC²，
即$\frac{4}{9}（2{x}^{2}+5）=4$，
解得：x=$\sqrt{2}$，
∴BN=$\sqrt{4+{x}^{2}}$=$\sqrt{6}$

点评 本题考查的知识点是三角形的五心，熟练掌握重心的性质，是解答的关键．