题目内容
15.设α,β为方程2x2-mx-2=0的两个根.其中m∈R且α<β.函数f(x)=$\frac{4x-m}{{x}^{2}+1}$.(1)求f(α)•f(β)的值:
(2)求证:函数f(x)在[α,β]上为增函数.
分析 ( 1)由题意并根据一元二次方程根与系数的关系可得α+β=$\frac{m}{2}$,αβ=-1,运算可得f(α)•f(β)的值.
(2)?x1,x2∈[α,β],x1<x2,依据条件判断f(x1)-f(x2)<0,从而得到函数f(x)在[α,β]上为增函数.
解答 解:(1)由题意可得α+β=$\frac{m}{2}$,αβ=-1,
f(α)•f(β)=$\frac{4α-m}{{α}^{2}+1}•\frac{4β-m}{{β}^{2}+1}$=$\frac{16αβ-4m(α+β)+{m}^{2}}{(αβ)^{2}+(α+β)^{2}-2αβ+1}$=-4.
证明:(2)?x1,x2∈[α,β],x1<x2,可得f(x1)-f(x2)=$\frac{({x}_{2}-{x}_{1})[4{x}_{1}{x}_{2}-4-m({x}_{2}+{x}_{1})]}{({{x}_{1}}^{2}+1)({{x}_{2}}^{2}+1)}$.
∵(x1-α)(x2-β)≤0,(x1-β)(x2-α)<0,
两式相加可得 2x1x2-(α+β)(x1+x2)+2αβ<0.
∵α+β=$\frac{m}{2}$,αβ=-1,
∴(x2-x1)[4x1x2-4-m(x2+x1)]<0,
∴f(x1)-f(x2)<0,
∴函数f(x)在[α,β]上为增函数.
点评 本题主要考查函数单调性的证明以及一元二次函数根与系数之间的关系,利用定义法是解决本题的关键.

练习册系列答案
相关题目
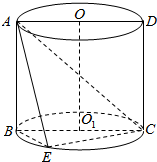 如图:已知矩形ABCD是圆柱OO1的轴截面,E是下底面圆周上的一点.
如图:已知矩形ABCD是圆柱OO1的轴截面,E是下底面圆周上的一点.