题目内容
11.已知f(x)=x2-1,g(x)=$\left\{\begin{array}{l}{x-1(x≥0)}\\{2-x(x<0)}\end{array}\right.$.求f[g(x)]和g[f(x)].分析 已知f(x)=x2-1,g(x)=$\left\{\begin{array}{l}x-1(x≥0)\\ 2-x(x<0)\end{array}\right.$,需要分类讨论,再利用整体法进行代入求解;
解答 解:∵f(x)=x2-1,g(x)=$\left\{\begin{array}{l}x-1(x≥0)\\ 2-x(x<0)\end{array}\right.$,
若x≥0,可得g(x)=x-1,可得f[g(x)]=(x-1)2-1=x2-2x;
若x<0,可得g(x)=2-x,可得f[g(x)]=(2-x)2-1=x2-4x+3;
∴f[g(x)]=$\left\{\begin{array}{l}{x}^{2}-2x,(x≥0)\\{x}^{2}-4x+3,(x<0)\end{array}\right.$;
∵f(x)=x2-1≥-1,
若x≥1或x≤-1,可得x2-1≥0,
∴g[f(x)]=x2-1-1=x2-2;
若-1<x<1,可得x2-1<0,
∴g[f(x)]=2-(x2-1)=-x2+3;
∴g[f(x)]=$\left\{\begin{array}{l}{x}^{2}-2,(x≥1或x≤-1)\\{-x}^{2}+3,(-1<x<1)\end{array}\right.$;
点评 此题主要考查函数的解析式的求解问题,整体法是一个常用的方法,是一道基础题;

练习册系列答案
相关题目
1.设f′(x)是f(x)的导函数,如果f′(x)是二次函数,且f′(x)的图象开口向上,顶点坐标为(1,$\sqrt{3}$),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
| A. | [$\frac{π}{3}$,π) | B. | ($\frac{π}{2},\frac{2π}{3}$] | C. | [$\frac{π}{3},\frac{π}{2}$) | D. | (0,$\frac{π}{3}$] |
2.若x-y-z=3,yz-xy-xz=3,则x2+y2+z2=( )
| A. | 0 | B. | 3 | C. | 9 | D. | -1 |
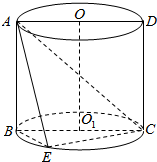 如图:已知矩形ABCD是圆柱OO1的轴截面,E是下底面圆周上的一点.
如图:已知矩形ABCD是圆柱OO1的轴截面,E是下底面圆周上的一点.