题目内容
【题目】手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式.在某市,随机调查了200名顾客购物时使用手机支付的情况,得到如下的2×2列联表,已知从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(I)根据已知条件完成2×2列联表,并根据此资料判断是否有99.5%的把握认为“市场购物用手机支付与年龄有关”?
2×2列联表:
青年 | 中老年 | 合计 | |
使用手机支付 | 120 | ||
不使用手机支付 | 48 | ||
合计 | 200 |
(Ⅱ)现采用分层抽样的方法从这200名顾客中按照“使用手机支付”和“不使用手机支付”抽取一个容量为10的样本,再从中随机抽取3人,求这三人中“使用手机支付”的人数的分布列及期望.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
【答案】(I)有99.5%的把握认为“市场购物用手机支付与年龄有关”
(Ⅱ)所求随机变量![]() 的概率分布为
的概率分布为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
期望![]()
【解析】
(Ⅰ)根据抽样比例求得对应数据,填写2×2列联表,根据表中数据计算K2,对照临界值得出结论;
(Ⅱ)根据分层抽样方法计算对应人数,得出随机变量X的可能取值,计算对应的概率值,写出X的分布列,计算数学期望值.
(Ⅰ)从使用手机支付的人群中随意抽取1人,抽到青年的概率为![]() ,
,
∴使用手机支付的人群中青年的人数为![]() 120=84,
120=84,
则使用手机支付的人群中的中老年的人数为120﹣84=36,
由此填写2×2列联表如下;
青年 | 中老年 | 合计 | |
使用手机支付 | 84 | 36 | 120 |
不使用手机支付 | 32 | 48 | 80 |
合计 | 116 | 84 | 200 |
根据表中数据,计算K2![]() 17.734>7.879,
17.734>7.879,
∴P(K2≥7.879)=0.005,
由此判断有99.5%的把握认为“市场购物用手机支付与年龄有关”;
(Ⅱ)根据分层抽样方法,从这200名顾客中抽取10人,
抽到“使用手机支付”的人数为10![]() 6,
6,
“不使用手机支付”的人数为4,
设随机抽取的3人中“使用手机支付”的人数为随机变量X,
则X的可能取值分别为0,1,2,3;
计算P(X=0)![]() ,
,
P(X=1)![]() ,
,
P(X=2)![]() ,
,
P(X=3)![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
X的数学期望为EX=0![]() 1
1![]() 2
2![]() 3
3![]() .
.

【题目】越接近高考学生焦虑程度越强,四个高三学生中大约有一个有焦虑症,经有关机构调查,得出距离高考周数与焦虑程度对应的正常值变化情况如下表:
周数x | 6 | 5 | 4 | 3 | 2 | 1 |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
(1)作出散点图:

(2)根据上表数据用最小二乘法求出y关于x的线性回归方程 (精确到0.01);
(3)根据经验,观测值为正常值的0.85~1.06为正常,若1.06~1.12为轻度焦虑,1.12~1.20为中度焦虑,1.20及其以上为重度焦虑,若为中度焦虑及其以上,则要进行心理疏导,若一个学生在距高考第二周时观测值为100,则该学生是否需要进行心理疏导?
(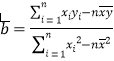 ,
, ![]() )
)