题目内容
20.若对于函数f(x)=$\frac{sin|x|}{x}$+b,现给出四个命题:①b=0时,f(x)为奇函数;
②y=f(x)的图象关于(0,b)对称;
③b=-1时,方程f(x)=0有且只有一个实数根;
④b=-1时,不等式f(x)>0的解集为空集.
其中正确的命题是①②④.(写出所有正确命题的编号)
分析 分析函数(x)=$\frac{sin|x|}{x}$的奇偶性,可判断①;结合函数图象的平移变换法则和①中结论,可判断②;根据方程sin|x|=x有且只有一个实根0,但0为方程f(x)=0的增根,可判断③;分类讨论$\frac{sin|x|}{x}$>1解集的情况,可判断④
解答 解:①b=0时,f(x)=$\frac{sin|x|}{x}$,f(-x)=$\frac{sin|-x|}{-x}$=$\frac{sin|x|}{-x}$=-$\frac{sin|x|}{x}$,满足f(-x)=-f(x)为奇函数,即①正确;
②y=f(x)的图象,由y=$\frac{sin|x|}{x}$的图象向上平移b个单位得到,由①知y=$\frac{sin|x|}{x}$的图象关于原点对称,故y=f(x)的图象关于(0,b)对称,即②正确;
③方程sin|x|=x有且只有一个实根0,但x=0时,$\frac{sin|x|}{x}$=1,无意义,即b=-1时,方程f(x)=0无实数根,即③错误;
④当x>0时,sin|x|>x的解集为空集,即$\frac{sin|x|}{x}$>1,的解集为空集,即f(x)>0的解集为空集.
当x<0时,sin|x|<x的解集为空集,即$\frac{sin|x|}{x}$>1,的解集为空集,即f(x)>0的解集为空集.
综上,b=-1时,不等式f(x)>0的解集为空集.故④正确
故正确的命题是:①②④;
故答案为:①②④
点评 本题以命题的真假判断为载体,考查了y=$\frac{sin|x|}{x}$的图象和性质,熟练掌握和理解y=$\frac{sin|x|}{x}$的图象和性质是解答的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
10.已知:a,b,c,d满足:log${\;}_{\frac{1}{2}}$a=3a,log${\;}_{\frac{1}{2}}$b=2b,$\frac{1}{{3}^{c}}$=log2c,$\frac{1}{{2}^{d}}$=log2d.则a,b,c,d的大小关系是( )
| A. | a>b>c>d | B. | a<b<c<d | C. | a>b>d>c | D. | b>a>c>d |
8.命题p:?x∈R,ex-mx=0,命题q:f(x)=$\frac{1}{3}$x3-mx2-2x在[-1,1]上递减,若(¬p)∧q为真命题,则实数m的取值范围为( )
| A. | [0,$\frac{1}{2}$] | B. | [-3,0] | C. | [-3,e) | D. | [0,e) |
15.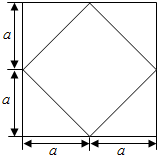 已知某个几何体的正视图、侧视图、俯视图均为如图所示的形状,根据图中标出的尺寸,可得这个几何体的体积是( )
已知某个几何体的正视图、侧视图、俯视图均为如图所示的形状,根据图中标出的尺寸,可得这个几何体的体积是( )
 已知某个几何体的正视图、侧视图、俯视图均为如图所示的形状,根据图中标出的尺寸,可得这个几何体的体积是( )
已知某个几何体的正视图、侧视图、俯视图均为如图所示的形状,根据图中标出的尺寸,可得这个几何体的体积是( )| A. | 8a3 | B. | $\frac{20}{3}$a3 | C. | 2$\sqrt{2}$a3 | D. | 5a3 |
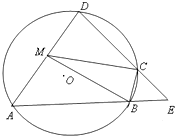 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.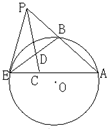 如图,过点P作圆O的割线PAB与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,若∠AEB=30°,则∠PCE=75°.
如图,过点P作圆O的割线PAB与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,若∠AEB=30°,则∠PCE=75°.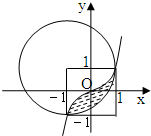 为了近似估计π的值,用计算机分别产生90个在[-1,1]的均匀随机数x1,x2,…,x90和y1,y2,…,y90,在90组数对(xi,yi)(1≤i≤90,i∈N*)中,
为了近似估计π的值,用计算机分别产生90个在[-1,1]的均匀随机数x1,x2,…,x90和y1,y2,…,y90,在90组数对(xi,yi)(1≤i≤90,i∈N*)中,