题目内容
8.命题p:?x∈R,ex-mx=0,命题q:f(x)=$\frac{1}{3}$x3-mx2-2x在[-1,1]上递减,若(¬p)∧q为真命题,则实数m的取值范围为( )| A. | [0,$\frac{1}{2}$] | B. | [-3,0] | C. | [-3,e) | D. | [0,e) |
分析 首先求出函数=m=$\frac{{e}^{x}}{x}$的极值,进一步利用导数求出函数f(x)在[-1,1]递减的充要条件,最后利用p假q真求出m的交集即可.
解答 解:命题p:?x∈R,ex-mx=0,
则:m=$\frac{{e}^{x}}{x}$,
设g(x)=$\frac{{e}^{x}}{x}$,
则:g′(x)=$\frac{(x-1){e}^{x}}{{x}^{2}}$
当x>1时,g′(x)>0,函数g(x)为单调递增函数.
当0<x<1时,g′(x)<0,函数g(x)为单调递减函数.
当x<0时,g′(x)<0,函数g(x)为单调递减函数.
所以:当x=1时函数g(x)取极小值,g(1)=e.
所以:函数g(x)的值域为:(-∞,0)∪[e,+∞).
即:m∈(-∞,0)∪[e,+∞).
命题q:f(x)=f(x)=$\frac{1}{3}$x3-mx2-2x-mx2-2x在[-1,1]递减,
所以:f′(x)=x2-2mx-2
由于函数f(x)在[-1,1]递减,
所以:$\left\{\begin{array}{l}{f′(-1)≤0}\\{f′(1)≤0}\end{array}\right.$,
解得:$-\frac{1}{2}$≤m≤$\frac{1}{2}$,
由(¬p)∧q为真命题,
则:p假q真,
所以$\left\{\begin{array}{l}{0≤m<e}\\{-\frac{1}{2}≤m≤\frac{1}{2}}\end{array}\right.$:,
解得0≤m≤$\frac{1}{2}$:
故选:A
点评 本题考查的知识要点:利用函数的导数求函数的单调区间和极值,主要考查学生的应用能力,属于中档题.

练习册系列答案
相关题目
18.若函数f(x)=ax3+ax2+x-1在实数R上是增函数,则实数a的取值范围是( )
| A. | [-1,2] | B. | [0,3] | C. | [2,5] | D. | (0,3) |
19.在等腰△ABC中,角A,B,C的对边分别为a,b,c,若sinB=sinAcosC-$\frac{1}{2}$sinC,且a=$\sqrt{3}$,则△ABC的面积为( )
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | ||
| C. | $\sqrt{3}$ | D. | 条件不足,无法计算 |
16.已知函数f(x)满足f(0)=1,且对于任意实数x,y∈R都有:f(xy+1)=f(x)f(y)-f(y)-x+2,若x∈[1,3],则$\frac{f(x-1)}{{f}^{2}(x)+1}$的最大值为( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{17}$ |
13.已知M={x|x2-x=0},N={y|y2+y=0},则M∩N=( )
| A. | {-1,1,0} | B. | {-1,1} | C. | {0} | D. | ∅ |
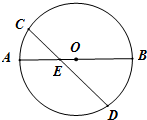 设AB为圆O的直径,AB=10.E为线段AO上一点,OE=$\frac{1}{7}$AB.过E作一直线交圆O于C,D两点,使得∠CEA=45°.试求CE2+ED2的值.
设AB为圆O的直径,AB=10.E为线段AO上一点,OE=$\frac{1}{7}$AB.过E作一直线交圆O于C,D两点,使得∠CEA=45°.试求CE2+ED2的值.