题目内容
12.若数列{an}满足:a1=1,an+1=an+n2,求数列{an}的通项公式.分析 将条件转化为an+1-an=n2,用累计法.
解答 解:a1=1,an+1=an+n2,
∴an+1-an=n2,
∴n=1时,a2-a1=12,
n=2时,a3-a2=22,
…
n=n-1时,an-an-1=(n-1)2,
∴an-a1=12+22+…+(n-1)2=$\frac{1}{6}$n(n-1)(2n-1),
∴an=a1+$\frac{1}{6}$n(n-1)(2n-1)=1+$\frac{1}{6}$n(n-1)(2n-1).
点评 本题主要考查用累计法求通项公式并应用公式12+22+…+(n-1)2+n2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知全集U=R,集合A={x|${\frac{x-1}{x+3}$≤0},集合B={x|y=$\sqrt{3-{{(\frac{1}{3})}^x}}$,x∈R},则A∩(CUB)为( )
| A. | {x|-3<x≤-1} | B. | {x|-3≤x<-1} | C. | {x|-3≤x≤-1} | D. | {x|-3<x<-1} |
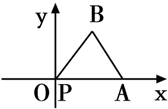 将边长为2的等边△PAB沿x轴正方向滚动,某时刻P与坐标原点重合(如图),设顶点P(x,y)的轨迹方程是y=f(x),关于函数y=f(x)的有下列说法:
将边长为2的等边△PAB沿x轴正方向滚动,某时刻P与坐标原点重合(如图),设顶点P(x,y)的轨迹方程是y=f(x),关于函数y=f(x)的有下列说法: