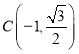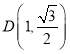题目内容
【题目】某共享单车经营企业欲向甲市投放单车,为制定适宜的经营策略,该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段,![]() ,
,![]() 两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
组别 年龄 |
|
| ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本,再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.
①求这60人中“年龄达到35岁且偶尔使用单车”的人数;
②为听取对发展共享单车的建议,调查组专门组织所抽取的“年龄达到35岁且偶尔使用单车”的人员召开座谈会.会后共有3份礼品赠送给其中3人,每人1份(其余人员仅赠送骑行优惠券).已知参加座谈会的人员中有且只有4人来自![]() 组,求
组,求![]() 组这4人中得到礼品的人数
组这4人中得到礼品的人数![]() 的分布列和数学期望;
的分布列和数学期望;
(2)从统计数据可直观得出“是否经常使用共享单车与年龄(记作![]() 岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄
岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄![]() 应取25还是35?请通过比较
应取25还是35?请通过比较![]() 的观测值的大小加以说明.
的观测值的大小加以说明.
参考公式: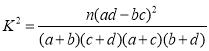 ,其中
,其中![]() .
.
【答案】(1) ①9人 ②见解析;(2) ![]()
【解析】
(1)①根据分层抽样要求,先求从300人中抽取60人,其中“年龄达到35岁”的人数![]() ,再求“年龄达到35岁” 中偶尔使用单车的人数
,再求“年龄达到35岁” 中偶尔使用单车的人数![]() ;
;
②确定随机变量X的取值,计算X各个取值的概率,得分布列及数学期望.
(2)对年龄m是否达到35,m是否达到25对数据重新整理(2![]() 2联表),根据公式计算相应的
2联表),根据公式计算相应的![]() ,比较大小确定.
,比较大小确定.
(1)①从300人中抽取60人,其中“年龄达到35岁”的有![]() 人,再将这20人用分层抽样法按“是否经常使用单车”进行名额划分,其中“年龄达到35岁且偶尔使用单车”的人数为
人,再将这20人用分层抽样法按“是否经常使用单车”进行名额划分,其中“年龄达到35岁且偶尔使用单车”的人数为![]() .
.
②![]() 组这4人中得到礼品的人数
组这4人中得到礼品的人数![]() 的可能取值为0,1,2,3,相应概率为:
的可能取值为0,1,2,3,相应概率为:
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
故其分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.
(2)按“年龄是否达到35岁”对数据进行整理,得到如下列联表:
经常使用单车 | 偶尔使用单车 | 合计 | |
未达到35岁 | 125 | 75 | 200 |
达到35岁 | 55 | 45 | 100 |
合计 | 180 | 120 | 300 |
![]() 时,由(1)中的列联表,可求得
时,由(1)中的列联表,可求得![]() 的观测值
的观测值
![]() .
.
![]() 时,按“年龄是否达到25岁”对数据进行整理,得到如下列联表:
时,按“年龄是否达到25岁”对数据进行整理,得到如下列联表:
经常使用单车 | 偶尔使用单车 | 合计 | |
未达到25岁 | 67 | 33 | 100 |
达到25岁 | 113 | 87 | 200 |
合计 | 180 | 120 | 300 |
可求得![]() 的观测值
的观测值
![]() .
.
∴![]() ,
,
欲使犯错误的概率尽可能小,需取![]() .
.

【题目】某百货商店今年春节期间举行促销活动,规定消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商店经理对春节前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计,![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(1)经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.请根据上表提供的数据,用最小二乘法求出
具有线性相关关系.请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)该商店规定:若抽中“一等奖”,可领取600元购物券;抽中“二等奖”可领取300元购物券;抽中“谢谢惠顾”,则没有购物券.已知一次抽奖活动获得“一等奖”的概率为![]() ,获得“二等奖”的概率为
,获得“二等奖”的概率为![]() .现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额
.现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:,
![]() ,
,![]() ,
,![]() .
.
【题目】为庆祝新中国成立七十周年,巴蜀中学将举行“歌唱祖国,喜迎国庆”歌咏比赛活动,《歌唱祖国》,《精忠报国》,《我和我的祖国》等一系列歌曲深受同学们的青睐,高二某班级就该班是否选择《精忠报国》作为本班参赛曲目进行投票表决,投票情况如下表.
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
赞成人数 | 4 | 5 | 6 | 6 | 5 | 6 | 4 | 3 |
总人数 | 7 | 7 | 8 | 8 | 7 | 7 | 6 | 6 |
(1)若从第1小组和第8小组的同学中各随机选取2人进行调查,求所选取的4人中至少有2人赞成《精忠报国》作为本班参赛曲目的概率;
(2)若从第5小组和第7小组的同学中各随机选取2人进行调查,记选取的4人中不赞成《精忠报国》作为本班参赛曲目的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.