题目内容
【题目】如图，在多面体
中，四边形
是菱形，
，
，
，
平面，
，
，
是
的中点.
（1）求证：平面
平面
；
（2）求直线
与平面
所成的角的正弦值.
【答案】(Ⅰ)详见解析；(Ⅱ)
．
【解析】试题分析：（Ⅰ）连接
交
于
，得
，所以
面
，又
，得
面，即可利用面面平行的判定定理，证得结论；
（Ⅱ）如图，以O为坐标原点，建立空间直角坐标系，求的平面
的一个法向量
，利用向量
和向量夹角公式，即可求解与平面所成角的正弦值．
试题解析：
（Ⅰ）连接BD交AC于O，易知O是BD的中点，故OG//BE，BE
面BEF，OG在面BEF外，所以OG//面BEF；
又EF//AC，AC在面BEF外，AC//面BEF，又AC与OG相交于点O，面ACG有两条相交直线与面BEF平行，故面ACG∥面BEF；
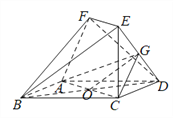
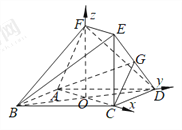
（Ⅱ）如图，以O为坐标原点，分别以OC、OD、OF为x、y、z轴建立空间直角坐标系，则
，
， 
，
， 
，
，
，
设面ABF的法向量为
，依题意有
，
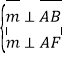，令
，
，
，
，
，
直线AD与面ABF成的角的正弦值是．
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】某地区2020年清明节前后3天每天下雨的概率为60%，通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率：用随机数
（
，且
）表示是否下雨：当
时表示该地区下雨，当
时，表示该地区不下雨，从随机数表中随机取得20组数如下
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
（1）求出
的值，并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率；
（2）从2011年开始到2019年该地区清明节当天降雨量（单位：
）如下表：（其中降雨量为0表示没有下雨）.
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明：从2011年开始至2020年， 该地区清明节有降雨的年份的降雨量
与年份
成线性回归，求回归直线
，并计算如果该地区2020年（
）清明节有降雨的话，降雨量为多少？（精确到0.01）
参考公式：
.
参考数据：
，
，
，
.
【题目】某共享单车经营企业欲向甲市投放单车，为制定适宜的经营策略，该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段，
，
两个调查小组分赴全市不同区域发放问卷并及时收回；在整理分析阶段，两个调查小组从所获取的有效问卷中，针对15至45岁的人群，按比例随机抽取了300份，进行了数据统计，具体情况如下表：
组别 年龄 |
|
| ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
（1）先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本，再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.
①求这60人中“年龄达到35岁且偶尔使用单车”的人数；
②为听取对发展共享单车的建议，调查组专门组织所抽取的“年龄达到35岁且偶尔使用单车”的人员召开座谈会.会后共有3份礼品赠送给其中3人，每人1份（其余人员仅赠送骑行优惠券）.已知参加座谈会的人员中有且只有4人来自组，求组这4人中得到礼品的人数
的分布列和数学期望；
（2）从统计数据可直观得出“是否经常使用共享单车与年龄（记作
岁）有关”的结论.在用独立性检验的方法说明该结论成立时，为使犯错误的概率尽可能小，年龄应取25还是35？请通过比较
的观测值的大小加以说明.
参考公式：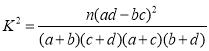
，其中
.
