题目内容
20．已知△ABC中，a=7，b=8，A=60°，则边c=3或5．．分析 利用余弦定理得出a2=b2+c2-2bccosA，把已知a，b及A的度数代入，利用特殊角的三角函数值化简，得出关于c的一元二次方程，求出方程的解即可得到c的值．
解答 解：∵在△ABC，a=7，b=8，A=60°，
∴根据余弦定理a2=b2+c2-2bc•cosA得：72=82+c2-16c•cos60°，
整理得：c2-8c+15=0，
解得：c=3或c=5，
则c的值为3或5．
故答案为：3或5．
点评 此题考查了余弦定理，一元二次方程的解法，以及特殊角的三角函数值，余弦定理很好的建立了三角形的边角关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
19．“x＜2”是“x（x-1）＜0”成立的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
20．
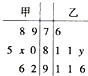某中学高一级从甲、乙两个班中各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的众数是80，乙班学生成绩的中位数是89，则x+y的值为（ ）
某中学高一级从甲、乙两个班中各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的众数是80，乙班学生成绩的中位数是89，则x+y的值为（ ）| A． | 7 | B． | 8 | C． | 9 | D． | 14 |
8．已知集合M={2，3，4}，N={0，2，3，5}，则M∪N中元素的个数为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
12．复平面上有点A，B其对应的复数分别为-3+i和-1-3i，O为原点，那么△AOB是（ ）
| A． | 直角三角形 | B． | 等腰三角形 | C． | 等腰直角三角形 | D． | 正三角形 |