题目内容
5.已知点列(an,an+1)(n∈N*)在函数f(x)=-$\frac{1}{x+2}$的图象上,a1=f(0)且bn=$\frac{1}{{a}_{n}+1}$.(1)求b1,b2,b3,b4;
(2)根据以上的结果猜想bn的表达式,并证明.
分析 (1)运用代入法和点满足函数式,计算即可得到所求值;
(2)猜想bn=n+1.再由等差数列的定义,作差化简,整理即可得到常数1,即可得证.
解答 解:(1)由题意可得,a1=f(0)=-$\frac{1}{2}$,
且bn=$\frac{1}{{a}_{n}+1}$,即有b1=$\frac{1}{{a}_{1}+1}$=2,
(an,an+1)(n∈N*)在函数f(x)=-$\frac{1}{x+2}$的图象上,
an+1=-$\frac{1}{{a}_{n}+2}$,
a2=-$\frac{1}{{a}_{1}+2}$=-$\frac{2}{3}$,b2=$\frac{1}{{a}_{2}+1}$=3,
a3=-$\frac{3}{4}$,b3=$\frac{1}{{a}_{3}+1}$=4,
a4=-$\frac{4}{5}$,b4=5;
(2)猜想bn=n+1.
证明:bn+1-bn=$\frac{1}{1+{a}_{n+1}}$-$\frac{1}{1+{a}_{n}}$
=$\frac{1}{-\frac{1}{2+{a}_{n}}+1}$-$\frac{1}{{a}_{n}+1}$=$\frac{{a}_{n}+2}{{a}_{n}+1}$-$\frac{1}{{a}_{n}+1}$=1,
由a1=-$\frac{1}{2}$,b1=2,
又{bn}是以2为首项,1为公差的等差数列;
即有bn=n+1.
点评 本题考查等差数列的定义和通项公式,同时考查函数与数列的关系,考查运算能力,属于中档题.

练习册系列答案
相关题目
13.全集U={0,1,2,3,5,6,8 },集合A={ 1,5,8 },B={ 2 },则集合(∁UA)∪B为( )
| A. | { 0,2,3,6 } | B. | { 0,3,6 } | C. | { 1,2,5,8 } | D. | ∅ |
17.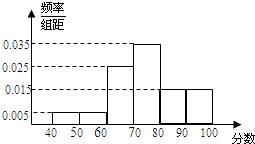 某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示.则不低于60分的人数是( )
某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示.则不低于60分的人数是( )
 某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示.则不低于60分的人数是( )
某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示.则不低于60分的人数是( )| A. | 800 | B. | 900 | C. | 950 | D. | 990 |
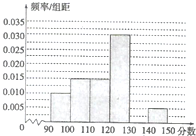 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为90分至150分之间的整数)分成六组[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为90分至150分之间的整数)分成六组[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: