题目内容
.(本小题满分14分)
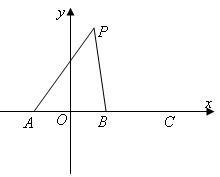
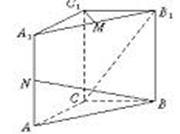
如图所示,在直角梯形ABCD中,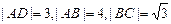 ,曲线段.DE上
,曲线段.DE上
任一点到A、B两点的距离之和都相等.
(Ⅰ) 建立适当的直角坐标系,求曲线段DE的方程;
(Ⅱ) 过C能否作-条直线与曲线段DE 相交,且所
得弦以C为中点,如果能,求该弦所在的直线
的方程;若不能,说明理由.
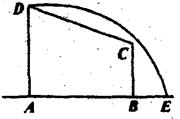
如图所示,在直角梯形ABCD中,
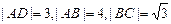 ,曲线段.DE上
,曲线段.DE上任一点到A、B两点的距离之和都相等.
(Ⅰ) 建立适当的直角坐标系,求曲线段DE的方程;
(Ⅱ) 过C能否作-条直线与曲线段DE 相交,且所
得弦以C为中点,如果能,求该弦所在的直线
的方程;若不能,说明理由.

解:(Ⅰ)以直线AB为x轴,线段AB的中点为原点建立直角坐标系,则A(-2,0),B
(2,0),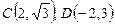 .依题意,曲线段DE是以A、B为焦点的椭圆的
.依题意,曲线段DE是以A、B为焦点的椭圆的
一部分. …………………………………………….3分
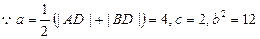
∴所求方程为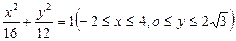 . ………………………6分
. ………………………6分
(Ⅱ)设这样的直线存在,
(1)当斜率不存在时,
(2)当直线的斜率存在时,其方程为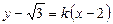 ,即
,即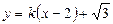
将其代入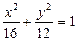 得
得
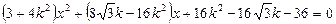 ……………………9分
……………………9分
设弦的端点为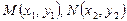 ,则由
,则由
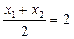 ,知x1+x2=4,
,知x1+x2=4,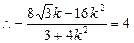 ,解得
,解得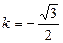 ……………l2分
……………l2分
∴弦MN所在直线方程为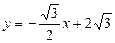
验证得知,这时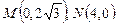 适合条件,
适合条件,
故这样的直线存在;其方程为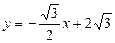 ……… 14分
……… 14分
(2,0),
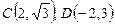 .依题意,曲线段DE是以A、B为焦点的椭圆的
.依题意,曲线段DE是以A、B为焦点的椭圆的一部分. …………………………………………….3分
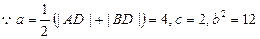
∴所求方程为
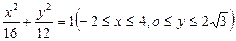 . ………………………6分
. ………………………6分(Ⅱ)设这样的直线存在,
(1)当斜率不存在时,
(2)当直线的斜率存在时,其方程为
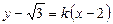 ,即
,即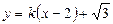
将其代入
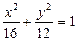 得
得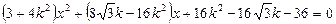 ……………………9分
……………………9分设弦的端点为
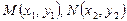 ,则由
,则由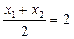 ,知x1+x2=4,
,知x1+x2=4,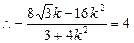 ,解得
,解得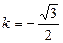 ……………l2分
……………l2分∴弦MN所在直线方程为
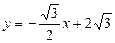
验证得知,这时
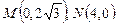 适合条件,
适合条件,故这样的直线存在;其方程为
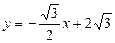 ……… 14分
……… 14分略

练习册系列答案
相关题目
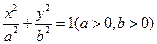 的右顶点为
的右顶点为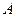 ,点
,点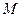 在椭圆上,且它的横坐标为1,点
在椭圆上,且它的横坐标为1,点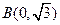 ,且
,且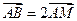 .
. 与椭圆交于另一点
与椭圆交于另一点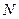 ,若线段
,若线段 的垂直平分线经过点
的垂直平分线经过点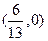 ,求直线
,求直线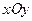 中,已知动点
中,已知动点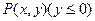 到点
到点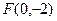 的距离为
的距离为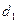 ,到
,到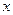 轴的距离为
轴的距离为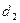 ,且
,且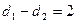 .
.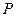 的轨迹
的轨迹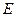 的方程;
的方程;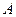 、
、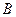 是(I)中
是(I)中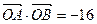 ,过
,过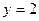 的垂线,垂足分别为
的垂线,垂足分别为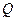 .证明:直线
.证明:直线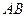 过定点
过定点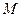 ,且
,且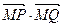 为定值.
为定值.
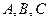 三点在
三点在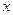 轴上,原点
轴上,原点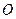 和点
和点 分别是线段
分别是线段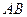 和
和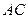 的中点,已知
的中点,已知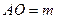 (
(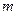 为常数),平面上的点
为常数),平面上的点 满
满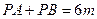 。
。
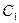 的方程;
的方程;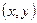 在曲线
在曲线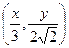 一定在某圆
一定在某圆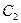 上;
上; 作直线
作直线 ,与圆
,与圆 两点,若点
两点,若点 恰好是线段
恰好是线段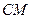 的中点,试求直线
的中点,试求直线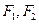 ,离心率为
,离心率为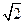 ,且过点
,且过点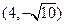 ,
,
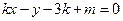 (其中
(其中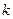 为参数)所过的定点
为参数)所过的定点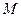 恰在双曲线上,求证:
恰在双曲线上,求证: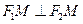 。
。 中,
中, ,若周长为16,则顶点
,若周长为16,则顶点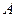 的轨迹方程为_________.
的轨迹方程为_________.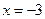 的距离小1,求点M满足的方程。
的距离小1,求点M满足的方程。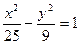 与椭圆
与椭圆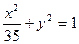 有相同的焦点;
有相同的焦点;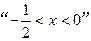 是“2x2-5x-3<0”必要不充分条件;
是“2x2-5x-3<0”必要不充分条件;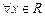 ,
,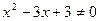 .
.