题目内容
(本小题12分)
已知双曲线的中心在原点,左右焦点分别为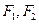 ,离心率为
,离心率为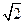 ,且过点
,且过点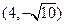 ,
,
(1)求此双曲线的标准方程;
(2)若直线系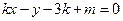 (其中
(其中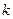 为参数)所过的定点
为参数)所过的定点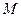 恰在双曲线上,求证:
恰在双曲线上,求证: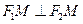 。
。
已知双曲线的中心在原点,左右焦点分别为
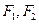 ,离心率为
,离心率为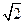 ,且过点
,且过点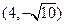 ,
,
(1)求此双曲线的标准方程;
(2)若直线系
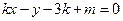 (其中
(其中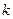 为参数)所过的定点
为参数)所过的定点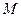 恰在双曲线上,求证:
恰在双曲线上,求证: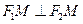 。
。
略

练习册系列答案
相关题目
题目内容
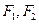 ,离心率为
,离心率为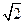 ,且过点
,且过点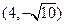 ,
,
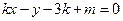 (其中
(其中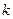 为参数)所过的定点
为参数)所过的定点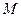 恰在双曲线上,求证:
恰在双曲线上,求证: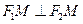 。
。
