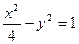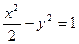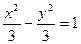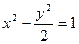题目内容
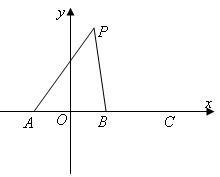
(本小题满分16分)如图,在直角坐标系中,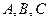 三点在
三点在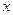 轴上,原点
轴上,原点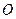 和点
和点 分别是线段
分别是线段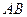 和
和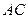 的中点,已知
的中点,已知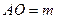 (
(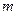 为常数),平面上的点
为常数),平面上的点 满
满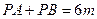 。
。
(1)试求点 的轨迹
的轨迹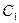 的方程;
的方程;
(2)若点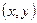 在曲线
在曲线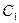 上,求证:点
上,求证:点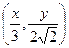 一定在某圆
一定在某圆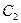 上;
上;
(3)过点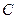 作直线
作直线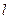 ,与圆
,与圆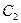 相交于
相交于 两点,若点
两点,若点 恰好是线段
恰好是线段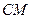 的中点,试求直线
的中点,试求直线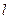 的方程。
的方程。
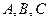 三点在
三点在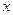 轴上,原点
轴上,原点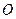 和点
和点 分别是线段
分别是线段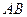 和
和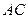 的中点,已知
的中点,已知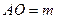 (
(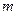 为常数),平面上的点
为常数),平面上的点 满
满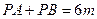 。
。
(1)试求点
 的轨迹
的轨迹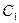 的方程;
的方程;(2)若点
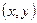 在曲线
在曲线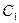 上,求证:点
上,求证:点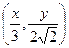 一定在某圆
一定在某圆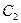 上;
上;(3)过点
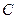 作直线
作直线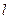 ,与圆
,与圆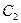 相交于
相交于 两点,若点
两点,若点 恰好是线段
恰好是线段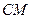 的中点,试求直线
的中点,试求直线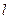 的方程。
的方程。⑴由题意可得点 的轨迹
的轨迹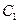 是以
是以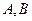 为焦点的椭圆. ……………………(2分)
为焦点的椭圆. ……………………(2分)
且半焦距长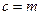 ,长半轴长
,长半轴长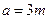 ,则
,则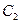 的方程为
的方程为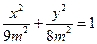 .………(5分)
.………(5分)
⑵若点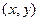 在曲线
在曲线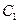 上,则
上,则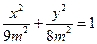 .设
.设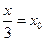 ,
,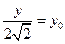 ,则
,则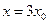 ,
,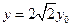 .…………………………………………………………………………(7分)
.…………………………………………………………………………(7分)
代入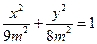 ,得
,得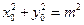 ,所以点
,所以点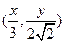 一定在某一圆
一定在某一圆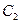 上.
上.
………………………………(10分)
⑶由题意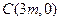 .………………………………………………………………(11分)
.………………………………………………………………(11分)
设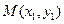 ,则
,则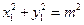 .┈┈┈①
.┈┈┈①
因为点 恰好是线段
恰好是线段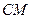 的中点,所以
的中点,所以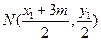 .代入
.代入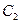 的方程得
的方程得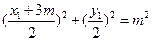 .┈┈┈②
.┈┈┈②
联立①②,解得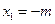 ,
,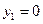 .…………………………………………………(15分)
.…………………………………………………(15分)
故直线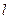 有且只有一条,方程为
有且只有一条,方程为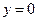 .……………………………………………(16分)
.……………………………………………(16分)
(若只写出直线方程,不说明理由,给1分)
 的轨迹
的轨迹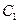 是以
是以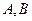 为焦点的椭圆. ……………………(2分)
为焦点的椭圆. ……………………(2分)且半焦距长
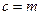 ,长半轴长
,长半轴长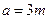 ,则
,则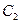 的方程为
的方程为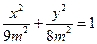 .………(5分)
.………(5分)⑵若点
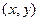 在曲线
在曲线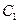 上,则
上,则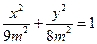 .设
.设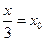 ,
,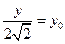 ,则
,则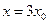 ,
,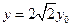 .…………………………………………………………………………(7分)
.…………………………………………………………………………(7分)代入
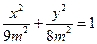 ,得
,得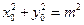 ,所以点
,所以点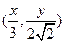 一定在某一圆
一定在某一圆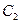 上.
上.………………………………(10分)
⑶由题意
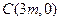 .………………………………………………………………(11分)
.………………………………………………………………(11分)设
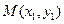 ,则
,则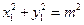 .┈┈┈①
.┈┈┈①因为点
 恰好是线段
恰好是线段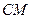 的中点,所以
的中点,所以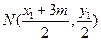 .代入
.代入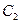 的方程得
的方程得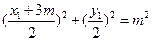 .┈┈┈②
.┈┈┈②联立①②,解得
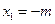 ,
,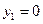 .…………………………………………………(15分)
.…………………………………………………(15分)故直线
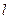 有且只有一条,方程为
有且只有一条,方程为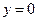 .……………………………………………(16分)
.……………………………………………(16分)(若只写出直线方程,不说明理由,给1分)
略

练习册系列答案
相关题目
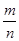 的大小有关
的大小有关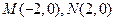 ,动点
,动点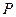 满足条件
满足条件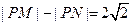 .记动点
.记动点 .
. 是
是 是坐标原点,求
是坐标原点,求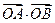 的最小值.
的最小值.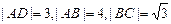 ,曲线段.DE上
,曲线段.DE上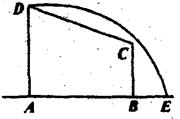
 ,
,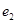 分别为具有公共焦点
分别为具有公共焦点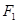 与
与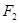 的椭圆和双曲线的离心率,
的椭圆和双曲线的离心率,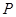 为两曲线的一个公共点,且满足
为两曲线的一个公共点,且满足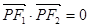 ,则
,则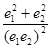 的值为
的值为 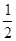
 所表示的曲线
所表示的曲线 )
)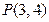 的动直线
的动直线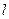 与
与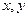 轴的交点分别为
轴的交点分别为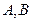 ,过
,过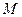 的轨迹方程为: .
的轨迹方程为: .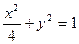 共焦点且过点P(2,1)的双曲线方程是( )
共焦点且过点P(2,1)的双曲线方程是( )