题目内容
（14分） 已知圆
方程为：
.
（1）直线
过点
，且与圆交于
、
两点，若
，求直线的方程；
（2）过圆上一动点
作平行于
轴的直线
，设与
轴的交点为
，若向量
（
为原点），求动点
的轨迹方程，并说明此轨迹是什么曲线.
解：（1）①当直线
垂直于
轴时，则此时直线方程为
，与圆的两个交点坐
标为
和
，其距离为
满足题意 …1分
②若直线不垂直于轴，设其方程为
，即
设圆心到此直线的距离为
，则
，得
……3分
∴
，
，
故所求直线方程为
综上所述，所求直线为或 …………7分
（2）设点
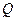的坐标为
（
），
点坐标为
则
点坐标是
…………9分
∵
，
∴
即
，
…………11分
又∵
，∴
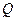∴点的轨迹方程是
， …13分
轨迹是一个焦点在
轴上的椭圆，除去长轴端点。 ……14分
解析
练习册系列答案
名校课堂系列答案
相关题目
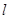经过点
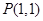，倾斜角
，
相交于A、B两点，求点P到A、B两点的距离之积.
与圆
相交于
两点，
的取值范围；
为坐标原点，且
，求
上，且与直线
相切，被直线
截得的弦长为
，求圆C的方程.
中，以
为圆心的圆与直线
相切．
轴相交于
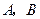两点，圆内的动点
使
成等比数列，求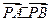
的取值范围（结果用区间表示）．:
，1＋
)，求直线l的方程；
＝0，P为圆M上任一点，求
＋
＋
的最值．
，以右顶点为圆心，实半轴长为半径的圆被双曲线的一条渐近线分为弧长为1：2的两部分，则双曲线的离心率为（ ）
：
，直线
被圆所截得的弦的中点为P（5，3）．
：
与圆