题目内容
(12分)一束光通过M(25,18)射入被x轴反射到圆C:x2+(y-7)2=25上.
(1)求通过圆心的反射光线所在的直线方程;
(2)求在x轴上反射点A的活动范围.
(1) x+y-7="0." (2) 从点(1,0)到点( ,0)的线段.
,0)的线段.
解析试题分析:(1)M(25,18)关于x轴的对称点为M′(25,-18)依题意,反射线所在直线过(25,-18),即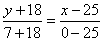 .
.
即x+y-7=0.
(2)设反射线所在直线为y+18=k(x-25).
即kx-y-25k-18=0.
依题意: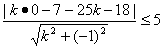 ,
,
解得: .
.
在①式中令y=0,得xA=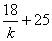 .
.
∵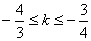 ,∴
,∴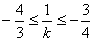 .
.
1≤xA≤ .
.
即在x轴上反射点A的活动范围是从点(1,0)到点( ,0)的线段.
,0)的线段.
考点:点关于直线对称;直线方程的点斜式;点到直线的距离公式;直线与圆的位置关系。
点评:本题注意考查对称点的求法。分析出反射光线一定过点M(25,18)关于x轴的对称点是做此题的关键。同时也考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 :
:
 为参数),圆
为参数),圆 (极轴与
(极轴与 轴的非负半轴重合,且单位长度相同)。
轴的非负半轴重合,且单位长度相同)。 到直线
到直线 ,求
,求 的值。
的值。 上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
 与两平行直线
与两平行直线 都相切,且圆心
都相切,且圆心 在直线
在直线 上,
上, 与
与 两点,
两点, 为坐标原点且满足
为坐标原点且满足 ,求直线
,求直线 (极轴与x轴的非负半轴重合,且单位长度相同)。
(极轴与x轴的非负半轴重合,且单位长度相同)。 的距离; (2)若直线
的距离; (2)若直线 的值。
的值。 :
: 的焦点为圆
的焦点为圆 的圆心,直线
的圆心,直线 与
与 交于不同的两点
交于不同的两点 .
. 。
。 .
. 时,求
时,求 的最大、最小值.
的最大、最小值. 方程为:
方程为: .
. 过点
过点 ,且与圆
,且与圆 、
、 两点,若
两点,若 ,求直线
,求直线 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 轴的交点为
轴的交点为 ,若向量
,若向量 (
( 为原点),求动点
为原点),求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.