题目内容
(本小题满分16分)
在直角坐标系xOy中,直线l与x轴正半轴和y轴正半轴分别相交于A,B两点,△AOB的内切圆为圆M.
(1)如果圆M的半径为1,l与圆M切于点C ( ,1+
,1+ ),求直线l的方程;
),求直线l的方程;
(2)如果圆M的半径为1,证明:当△AOB的面积、周长最小时,此时△AOB为同一个三角形;
(3)如果l的方程为x+y-2- =0,P为圆M上任一点,求
=0,P为圆M上任一点,求 +
+ +
+ 的最值.
的最值.
解析:(1)由题可得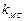 =
=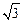 ,
,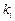 =
=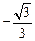 .所以l:y=
.所以l:y= +
+ +1.
+1.
(2)设A(a,0),B(0,b) (a>2,b>2),则l:bx+ay-ab=0.由题可得M (1,1).
所以点M到直线l的距离d=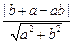 =1,整理得(a-2)(b-2)=2,即ab-2(a+b)+2=0.于是ab+2=2(a+b)≥
=1,整理得(a-2)(b-2)=2,即ab-2(a+b)+2=0.于是ab+2=2(a+b)≥ ,
,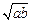 ≥2+
≥2+ ,ab≥6+
,ab≥6+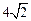 .当且仅当a=b=2+
.当且仅当a=b=2+ 时,ab=6+
时,ab=6+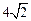 .
.
所以面积S=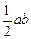 ≥3+
≥3+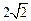 ,此时△AOB为直角边长为2+
,此时△AOB为直角边长为2+ 的等腰直角三角形.
的等腰直角三角形.
周长L=a+b+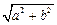 ≥
≥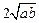 +
+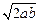 =(2+
=(2+ )·
)·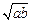 ≥
≥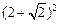 =6+
=6+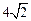 ,此时△AOB为直角边长为2+
,此时△AOB为直角边长为2+ 的等腰直角三角形.
的等腰直角三角形.
所以此时的△AOB为同一个三角形.
(3)l的方程为x+y-2- =0,得A(2+
=0,得A(2+ ,0),B(0,2+
,0),B(0,2+ ),
), :
: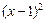 +
+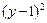 =1,设P(m,n)为圆上任一点,则
=1,设P(m,n)为圆上任一点,则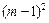 +
+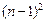 =1,
=1,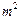 +
+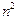 =2(m+n)-1,
=2(m+n)-1,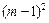 +
+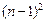 =1≥
=1≥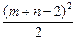 ,2-
,2- ≤m+n≤2+
≤m+n≤2+ .
. +
+ +
+ =
=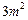 +
+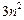 -(4+
-(4+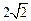 )(m+n)+
)(m+n)+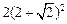 =(9+
=(9+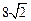 )-(
)-(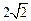 -2)(m+n).
-2)(m+n).
当m+n=2- 时,
时,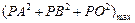 =(9+
=(9+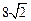 )-(
)-(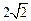 -2)( 2-
-2)( 2- )=17+
)=17+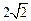 .此时,m=n=1-
.此时,m=n=1-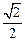 .
.
当m+n=2+ 时,
时,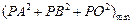 =(9+
=(9+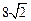 )-(
)-(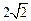 -2)( 2+
-2)( 2+ )=9+
)=9+ .此时,m=n=1+
.此时,m=n=1+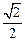 .
.
解析

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
若双曲线 的离心率为2,则
的离心率为2,则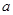 等于( )
等于( )
A. | B. | C. | D.1 |
 .
. 时,求
时,求 的最大、最小值.
的最大、最小值. 方程为:
方程为: .
. 过点
过点 ,且与圆
,且与圆 、
、 两点,若
两点,若 ,求直线
,求直线 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 轴的交点为
轴的交点为 ,若向量
,若向量 (
( 为原点),求动点
为原点),求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线. 过点
过点 ,圆
,圆 :
: .
.  ,求直线
,求直线 ),B(5,3),并且圆的面积被直线
),B(5,3),并且圆的面积被直线 :
: 平分.求圆C的方程;
平分.求圆C的方程; 的顶点坐标
的顶点坐标 ,直角顶点
,直角顶点 ,顶点
,顶点 在
在 轴上,点
轴上,点 为线段
为线段 的中点
的中点
 边所在直线方程;(2)圆
边所在直线方程;(2)圆 是△ABC的外接圆,求圆
是△ABC的外接圆,求圆 是否是定值?
是否是定值? 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )



 的直线l将圆
的直线l将圆 分成两段弧,当劣弧所对的圆心角最小时,求直线l的斜率。
分成两段弧,当劣弧所对的圆心角最小时,求直线l的斜率。