题目内容
设数列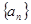 满足
满足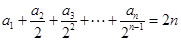 ,
,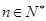 .
.
(1)求数列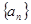 的通项公式;
的通项公式;
(2)设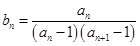 ,求数列
,求数列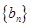 的前
的前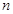 项和
项和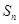 .
.
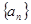 满足
满足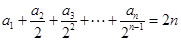 ,
,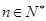 .
.(1)求数列
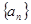 的通项公式;
的通项公式;(2)设
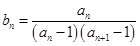 ,求数列
,求数列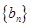 的前
的前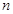 项和
项和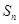 .
.(1)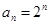 ;(2)
;(2)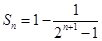 .
.
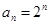 ;(2)
;(2)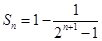 .
.试题分析:(1)先令
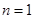 求出
求出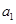 的值,然后令
的值,然后令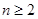 时,在原式中用
时,在原式中用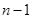 得到一个新的等式,并将该等式与原等式作差,求出数列
得到一个新的等式,并将该等式与原等式作差,求出数列 在
在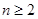 时的通项公式,并对
时的通项公式,并对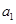 的值是否符合上述通项公式进行检验,从而最终确定数列
的值是否符合上述通项公式进行检验,从而最终确定数列 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列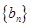 的通项公式
的通项公式 ,并根据数列
,并根据数列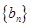 的通项公式结构选择裂项法求和.
的通项公式结构选择裂项法求和.试题解析:(1)因为
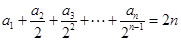 ,
,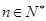 , ①
, ①所以当
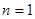 时,
时,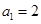 .
.当
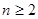 时,
时, , ② ,
, ② ,①-②得,
 ,所以
,所以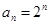 .
.因为
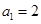 ,适合上式,所以
,适合上式,所以 ;
;(2)由(1)得
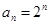 ,
,所以
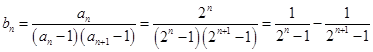 ,
,所以
 .
.
练习册系列答案
相关题目
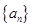 满足:
满足: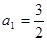 ,
, 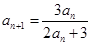
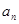 ;
;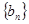 满足
满足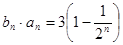 ,求数列
,求数列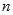 项和.
项和.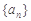 中,
中,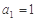 ,
,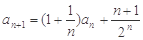 .
.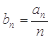 ,求数列
,求数列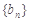 的通项公式;
的通项公式;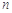 项和
项和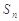 .
.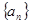 中,
中,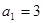 ,其前
,其前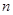 项和为
项和为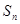 ,等比数列
,等比数列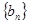 的各项均为正数,
的各项均为正数,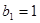 ,公比为
,公比为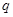 ,且
,且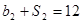 ,
,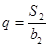 .
.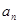 与
与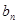 ;
;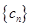 满足
满足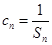 ,求
,求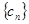 的前
的前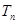 .
. 的前
的前 项和为
项和为 ,且
,且 ,
, ,数列
,数列 满足
满足 ,
, ,
, ;
; 的前
的前 .
. 的通项
的通项 ,其前n项和为
,其前n项和为 .
.  ;
; 求数列{
求数列{ }的前n项和
}的前n项和 .
.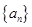 的前n项和
的前n项和 =
= -2n+1,则通项公式
-2n+1,则通项公式 =
=
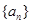 是由集合
是由集合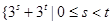 ,且
,且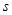 ,
,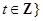 中所有的数从小到大排列成的数列,即
中所有的数从小到大排列成的数列,即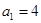 ,
,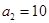 ,
,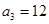 ,
,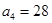 ,a5=30,a6=36,…,若
,a5=30,a6=36,…,若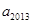 =
=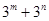
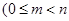 ,且
,且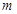 ,
,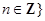 ,则
,则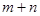 的值等于____________.
的值等于____________.