题目内容
(本小题满分13分)在等差数列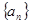 中,
中,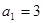 ,其前
,其前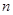 项和为
项和为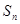 ,等比数列
,等比数列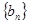 的各项均为正数,
的各项均为正数,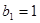 ,公比为
,公比为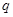 ,且
,且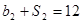 ,
,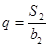 .
.
(1)求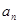 与
与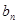 ;
;
(2)设数列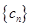 满足
满足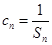 ,求
,求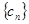 的前
的前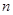 项和
项和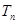 .
.
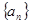 中,
中,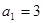 ,其前
,其前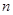 项和为
项和为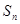 ,等比数列
,等比数列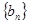 的各项均为正数,
的各项均为正数,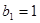 ,公比为
,公比为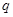 ,且
,且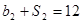 ,
,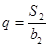 .
.(1)求
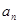 与
与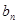 ;
;(2)设数列
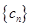 满足
满足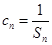 ,求
,求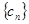 的前
的前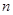 项和
项和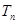 .
.(1)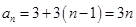 ,
,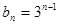 ;(2)
;(2) .
.
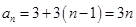 ,
,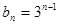 ;(2)
;(2) .
.试题分析:(1)由在等差数列
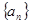 中,
中,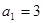 ,其前
,其前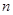 项和为
项和为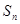 ,等比数列
,等比数列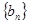 的各项均为正数,
的各项均为正数,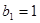 ,公比为
,公比为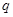 ,且
,且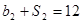 ,
,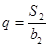 .列出两个关于公差和公比的方程.求出共差和公比即可求出等差数列和等比数列的通项.
.列出两个关于公差和公比的方程.求出共差和公比即可求出等差数列和等比数列的通项.(2)由(1)可得等差数列
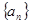 的通项公式所以可以求出前
的通项公式所以可以求出前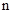 和
和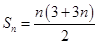 ,又因为
,又因为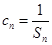 所以可得数列
所以可得数列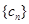 通项公式.再通过裂项求和可求得前
通项公式.再通过裂项求和可求得前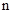 项和.
项和.试题解析:(1)设
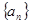 的公差为
的公差为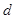 .
.因为
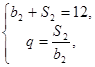 所以
所以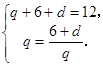 3分
3分解得
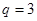 或
或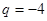 (舍),
(舍),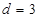 . 5分
. 5分故
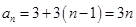 ,
,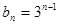 . 7分
. 7分(2)由(1)可知,
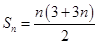 , 8分
, 8分所以
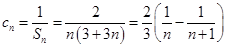 10分
10分故
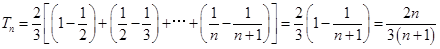 13分
13分
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
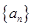 的前
的前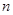 项和为
项和为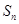 ,且满足
,且满足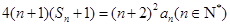 .
.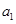 ,
,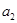 的值;
的值;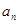 ;
;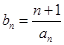 ,数列
,数列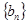 的前
的前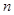 项和为
项和为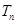 ,求证:
,求证: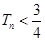 .
.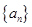 的前
的前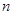 项和为
项和为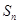 ,且
,且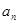 是
是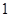 的等差中项,等差数列
的等差中项,等差数列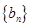 满足
满足
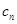 =
=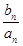 ,求数列
,求数列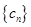 的前
的前 .
.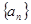 满足
满足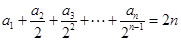 ,
,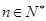 .
.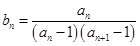 ,求数列
,求数列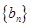 的前
的前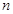 项和
项和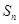 .
.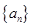 、
、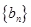 中,
中,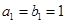 ,且当
,且当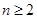 时,
时,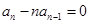 ,
,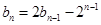 .记
.记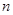 的阶乘
的阶乘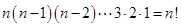 .
.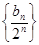 为等差数列;
为等差数列;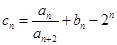 ,求
,求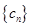 的前
的前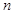 项和.
项和.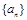 的前n项和为
的前n项和为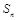 ,且
,且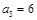 ,
,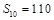 .
.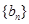 前n项和为
前n项和为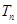 ,且
,且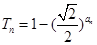 ,令
,令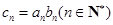 .求数列
.求数列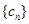 的前n项和
的前n项和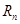 .
.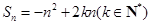 ,且
,且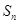 的最大值为4.
的最大值为4.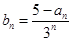 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与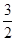 的大小.
的大小.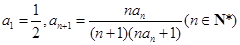 ,则数列{an}的前2012项的和为 .
,则数列{an}的前2012项的和为 .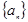 满足
满足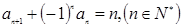 ,则数列
,则数列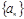 的前2016项的和
的前2016项的和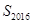 的值是___________.
的值是___________.