题目内容
ABCD是正方形,以BD为棱把它折成直二面角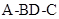 ,E为CD的中点,
,E为CD的中点,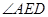 的大小为( )
的大小为( )
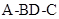 ,E为CD的中点,
,E为CD的中点,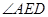 的大小为( )
的大小为( )A. | B. | C. | D. |
D
分析:由题意画出几何体的图形,设出正方形的边长,求出折叠后AD,AE,DE的长度,即可求出∠AED的大小。
解答:
由题意画出图形,

如图:

设正方形的边长为2,
折叠前后AD=2,DE=1,连接AC交BD于O,连接OE,则OE=1,AO=
 ,因为正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,
,因为正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,AO⊥BD,所以AO⊥平面BCD,所以AO⊥OE,
在△AOE中,AE2= AO2+OE2=3,
又AD=2,ED=1,所以DE2+AE2=AD2,
所以∠AED=90°,故选D。
点评:本题考查折叠问题,注意折叠前后,同一个半平面中的线线关系不变,考查空间想象能力计算能力,属中档题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
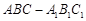 中已知
中已知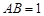 ,
,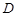 在棱
在棱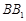 上,且
上,且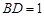 ,若
,若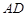 与平面
与平面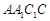 所成的角为
所成的角为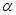 ,则
,则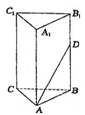




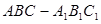 中,
中, 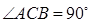 ,
,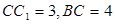 ,
, 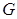 是
是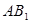 和
和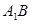 的交点, 若
的交点, 若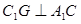 .
. 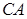 的长; (2)求点
的长; (2)求点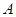 到平面
到平面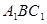 的距离;
的距离;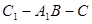 的平面角的正弦值的大小.
的平面角的正弦值的大小.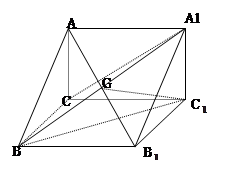
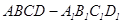 中,
中,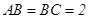 ,
,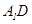 与
与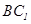
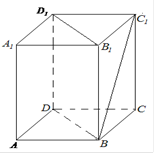
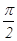 ,则
,则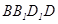 所成角的正弦值为( )
所成角的正弦值为( )







 的等腰直角三角形
的等腰直角三角形 与正三角形
与正三角形 所在平面互相垂直,
所在平面互相垂直, 是线段
是线段 的中点,则
的中点,则 与
与 所成角的大小为 .
所成角的大小为 .
 的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,
的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,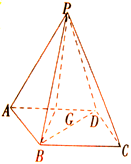
 中,
中, ,
, ,则
,则 与平面
与平面 所成角的正弦值为 .
所成角的正弦值为 .



