题目内容
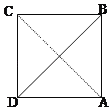
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.若
为正三角形.若![]() ,且
,且![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() .
.
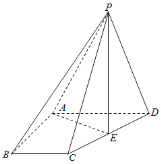
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 是线段
是线段![]() 上一点,记
上一点,记![]() ,是否存在实数
,是否存在实数![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见解析;(2)存在,![]()
【解析】
(1)由勾股定理与正三角形的性质可证![]() ,再由已知证得
,再由已知证得![]() ,由线面垂直的判定定理与面面垂直的判定定理即可证得平面
,由线面垂直的判定定理与面面垂直的判定定理即可证得平面![]() 平面
平面![]() ;
;
(2)作BC延长线于点Q,且BQ=AD,由(1)可知,QD,QP,QB两两垂直,以它们所在直线分别做x轴,y轴,z轴建立空间直角坐标系,结合已知即可表示点Q,A,C,D,E的坐标,进而求得面PAE与面ACE的法向量,利用向量的数量积求夹角与已知构建方程,求得![]() 的值.
的值.
(1)因为![]() ,
,![]() ,所以
,所以![]()
又因为![]() 为正三角形,所以
为正三角形,所以![]()
又![]() ,则
,则![]() ,即
,即![]()
又因为![]() ,
,![]() ,所以
,所以 ![]() 且
且![]()
所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]()
故平面![]()
![]() 平面
平面![]()
(2)作BC延长线于点Q,且BQ=AD,由(1)可知,QD,QP,QB两两垂直,以它们所在直线分别做x轴,y轴,z轴建立空间直角坐标系,则Q(0,0,0),A(2,2,0),C(0,1,0),D(2,0,0)
由![]() ,可得
,可得![]() ,所以
,所以![]()
设平面PAE的法向量为![]()
则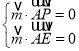 ,即
,即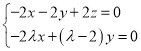 ,令
,令![]() ,解得
,解得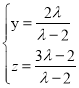
所以![]() ,显然
,显然![]() 是平面ACE的法向量
是平面ACE的法向量
设二面角![]() 为
为![]()
则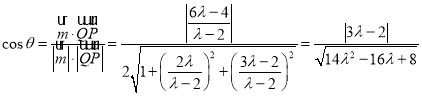
依据题意有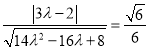 ,解得
,解得![]()

 名校课堂系列答案
名校课堂系列答案【题目】2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:

经济损失 4000元以下 | 经济损失 4000元以上 | 合计 | |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
(1)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(2)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,李师傅比张师傅早到小区的天数的数学期望.
附:临界值表
参考公式: ![]() .
.