题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若不等式![]() 对任意的
对任意的![]() 都成立,求实数m的取值范围.
都成立,求实数m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先利用导数求切线的斜率,再求切线方程;
(2) 根据题意可得![]() 对任意的
对任意的![]() ,
,![]() 都成立,
都成立,
当![]() 时,显然成立;当
时,显然成立;当![]() 时,设
时,设![]() , 问题即转化为
, 问题即转化为![]() 恒成立,只需要
恒成立,只需要![]() 即可,因为
即可,因为![]() (当且仅当
(当且仅当![]() 时取等号),即满足
时取等号),即满足![]() 即有
即有![]() 对
对![]() 恒成立,构造
恒成立,构造![]() ,通过求导判断函数的单调性求最小值,即可求得
,通过求导判断函数的单调性求最小值,即可求得![]() 的取值范围.
的取值范围.
(1)设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
∴函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(2)根据题意可得![]() 对任意的
对任意的![]() ,
,![]() 都成立,
都成立,
当![]() 时,不等式即为
时,不等式即为![]() ,显然成立;
,显然成立;
当![]() 时,设
时,设![]() ,则不等式
,则不等式![]() 恒成立,
恒成立,
即为不等式![]() 恒成立,
恒成立,
∵![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
∴由题意可得![]() ,即有
,即有![]() 对
对![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,
,
令![]() ,即有
,即有![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() 有且仅有一个根
有且仅有一个根![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
∴当![]() 时,
时,![]() 取得最小值,为
取得最小值,为![]() ,∴
,∴![]() .
.
∴实数![]() 的取值范围
的取值范围![]()

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】某次考试,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学物理分数对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
绘出散点图如下:

根据以上信息,判断下列结论:
①根据此散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据此散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③甲同学数学考了80分,那么,他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高.
其中正确的个数为( ).
A.0B.3C.2D.1
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: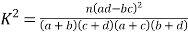
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |