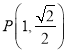题目内容

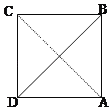
【题目】已知一个正四面体纸盒的俯视图如图所示，其中四边形ABCD是边长为的正方形，若在该正四面体纸盒内放一个正方体，使正方体可以在纸盒内任意转动，则正方体棱长的最大值是_____.

【答案】

【解析】

由一个正四面体纸盒的俯视图如图所示，其中四边形ABCD是边长为的正方形，

则正四面体的棱长，设此球的一个内接正方体的棱长为a，则，即可得答案.

由一个正四面体纸盒的俯视图如图所示，其中四边形ABCD是边长为的正方形，

则正四面体的棱长.

先求出此正四面体的内切球，再求出此球的一个内接正方体即可.

设此正四面体的应该内切球的半径为r，则4r S底面hS底面.

∴r.

作AO⊥底面BCD，垂足为O点，O为底面正三角形的中心.

AO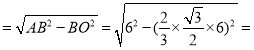2，∴r，

设此球的一个内接正方体的棱长为a，则，解得.

故答案为：.

练习册系列答案
相关题目

【题目】如图，在直三棱柱中， 分别是的中点.

（1）求证： 平面；

（2）若三棱柱的体积为4，求异面直线与夹角的余弦值.

【题目】如图，四棱锥中，，，，为正三角形.若，且与底面所成角的正切值为.

（1）证明：平面平面；

（2）是线段上一点，记，是否存在实数，使二面角的余弦值为？若存在，求出的值；若不存在，请说明理由.

【题目】如图，三棱锥中，点在以为直径的圆上，平面平面，点在线段上，且，，，，点为的重心，点为的中点.

（1）求证：平面；

（2）求点到平面的距离.

【题目】随着科技的发展，网络已逐渐融入了人们的生活．网购是非常方便的购物方式，为了了解网购在我市的普及情况，某调查机构进行了有关网购的调查问卷，并从参与调查的市民中随机抽取了男女各100人进行分析，从而得到表（单位：人）

经常网购

偶尔或不用网购

合计

男性

50

100

女性

70

100

合计

（1）完成上表，并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关？

（2）①现从所抽取的女市民中利用分层抽样的方法抽取10人，再从这10人中随机选取3人赠送优惠券，求选取的3人中至少有2人经常网购的概率；

②将频率视为概率，从我市所有参与调查的市民中随机抽取10人赠送礼品，记其中经常网购的人数为，求随机变量的数学期望和方差．

参考公式：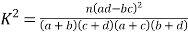

0.15

0.10

0.05

0.025

0.010

0.005

0.001

2.072

2.706

3.841

5.024

6.635

7.879

10.828

【题目】已知多面体中，、均垂直于平面，，，，是的中点．

（1）求证：平面；

（2）求直线与平面所成角的正弦值．

【题目】已知函数，

（1）当时，求函数在处的切线方程；

（2）若对任意的，都有恒成立，求a的取值范围；

（3）函数的图像上是否存在两点，且，使得直线AB的斜率k满足：？若存在，求出与之间的关系；若不存在，请说明理由.

【题目】已知椭圆：经过两点，.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）过椭圆的右焦点的直线交椭圆于，两点，且直线与以线段为直径的圆交于另一点（异于点），若，求直线的斜率.

【题目】2017年3月郑州市被国务院确定为全国46个生活垃圾分类处理试点城市之一，此后由郑州市城市管理局起草公开征求意见，经专家论证，多次组织修改完善，数易其稿，最终形成《郑州市城市生活垃圾分类管理办法》（以下简称《办法》）．《办法》已于2019年9月26日被郑州市人民政府第35次常务会议审议通过，并于2019年12月1日开始施行．《办法》中将郑州市生活垃圾分为厨余垃圾、可回收垃圾、有害垃圾和其他垃圾4类．为了获悉高中学生对垃圾分类的了解情况，某中学设计了一份调查问卷，500名学生参加测试，从中随机抽取了100名学生问卷，记录他们的分数，将数据分成7组：，，…，，并整理得到如下频率分布直方图：

（1）从总体的500名学生中随机抽取一人，估计其分数不低于60的概率；

（2）已知样本中分数小于40的学生有5人，试估计总体中分数在区间内的学生人数，

（3）学校环保志愿者协会决定组织同学们利用课余时间分批参加“垃圾分类，我在实践”活动，以增强学生的环保意识．首次活动从样本中问卷成绩低于40分的学生中随机抽取2人参加，已知样本中分数小于40的5名学生中，男生3人，女生2人，求抽取的2人中男女同学各1人的概率是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网