Question

【题目】若的三边长满足，则的取值范围为______．

Answer 1

【答案】

【解析】

设出x=，y=，根据b+2c≤3a，c+2a≤3b变形得到两个不等式，分别记作①和②，然后根据三角形的两边之和大于第三边，两边之差小于第三边分别列出不等式，变形得到三个不等式，分别记作③④⑤，画出图形，如图所示，得到由四点组成的四边形区域，根据简单的线性规划，得到x的范围，即得到的取值范围．

令x=，y=，由b+2c≤3a，c+2a≤3b得：

x+2y≤3①，3x﹣y≥2②，

又﹣c＜a﹣b＜c及a+b＞c得：

x﹣y＜1③，x﹣y＞﹣1④，x+y＞1⑤，

由①②③④⑤可作出图形，

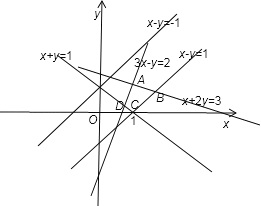
得到以点D（ ，），C（1，0），B（，），A（1，1）为顶点的四边形区域，

由线性规划可得：＜x＜，0＜y＜1，

则=x的取值范围为（，）．

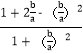∴= ==-1+=-1+ 在（，）上递减.

x= 时，原式= ，x=时，原式=

原式

故答案为：