题目内容
【题目】如图，AB是的⊙O直径，CB与⊙O相切于B，E为线段CB上一点，连接AC、AE分别交⊙O于D、G两点，连接DG交CB于点F． 
（1）求证：C、D、G、E四点共圆．
（2）若F为EB的三等分点且靠近E，EG=1，GA=3，求线段CE的长．
【答案】
（1）证明：连接BD，则∠AGD=∠ABD，
∵∠ABD+∠DAB=90°，∠C+∠CAB=90°
∴∠C=∠AGD，
∴∠C+∠DGE=180°，
∴C，E，G，D四点共圆．
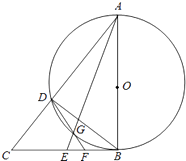
（2）解：∵EGEA=EB2，EG=1，GA=3，
∴EB=2，
又∵F为EB的三等分点且靠近E，
∴ 
， 
，
又∵FGFD=FEFC=FB2，
∴ 
，CE=2．
【解析】（1）连接BD，由题设条件结合圆的性质能求出∠C=∠AGD，从而得到∠C+∠DGE=180°，由此能证明C，E，G，D四点共圆．（2）由切割线定理推导出EB=2，由此能求出CE的长．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
