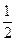题目内容
在数列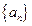 中,
中,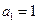 ,
,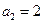 ,且
,且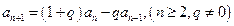 ;
;
(1)设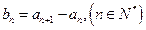 ,证明
,证明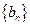 是等比数列;(2)求数列
是等比数列;(2)求数列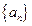 的通项公式;(3)若
的通项公式;(3)若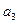 是
是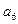 与
与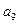 的等差中项,求
的等差中项,求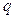 的值,并证明:对任意的
的值,并证明:对任意的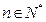 ,
,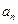 是
是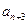 与
与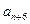 的等差中项;
的等差中项;
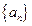 中,
中,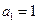 ,
,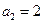 ,且
,且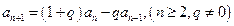 ;
;(1)设
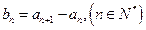 ,证明
,证明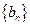 是等比数列;(2)求数列
是等比数列;(2)求数列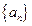 的通项公式;(3)若
的通项公式;(3)若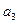 是
是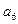 与
与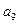 的等差中项,求
的等差中项,求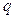 的值,并证明:对任意的
的值,并证明:对任意的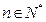 ,
,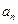 是
是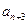 与
与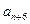 的等差中项;
的等差中项;(1)略(2) (3)证明略
(3)证明略
 (3)证明略
(3)证明略本题源自等差数列通项公式的推导。
(1)证明:由题设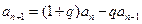 (
(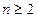 ),得
),得
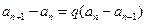 ,即
,即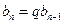 ,
,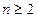 .
.
又 ,
,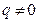 ,所以
,所以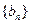 是首项为1,公比为
是首项为1,公比为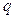 的等比数列.
的等比数列.
(2)由(1)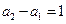 ,
,
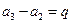 ,
,
……
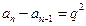 ,(
,(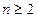 ).
).
将以上各式相加,得 (
(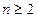 ).
).
所以当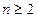 时,
时,
上式对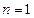 显然成立.
显然成立.
(3)由(2),当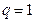 时,显然
时,显然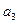 不是
不是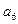 与
与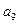 的等差中项,故
的等差中项,故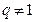 .
.
由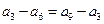 可得
可得 ,由
,由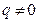 得
得 , ①
, ①
整理得 ,解得
,解得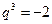 或
或 (舍去).于是
(舍去).于是 .
.
另一方面,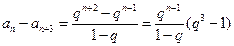 ,
,
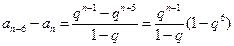 .
.
由①可得 ,
,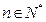 .
.
所以对任意的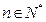 ,
,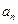 是
是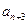 与
与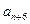 的等差中项.
的等差中项.
(1)证明:由题设
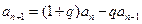 (
(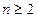 ),得
),得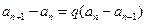 ,即
,即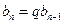 ,
,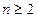 .
.又
 ,
,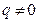 ,所以
,所以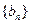 是首项为1,公比为
是首项为1,公比为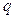 的等比数列.
的等比数列.(2)由(1)
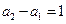 ,
,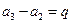 ,
,……
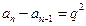 ,(
,(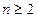 ).
).将以上各式相加,得
 (
(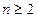 ).
).所以当
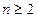 时,
时,
上式对
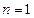 显然成立.
显然成立.(3)由(2),当
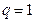 时,显然
时,显然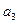 不是
不是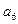 与
与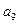 的等差中项,故
的等差中项,故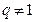 .
.由
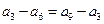 可得
可得 ,由
,由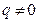 得
得 , ①
, ①整理得
 ,解得
,解得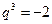 或
或 (舍去).于是
(舍去).于是 .
.另一方面,
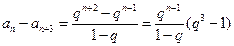 ,
,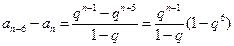 .
.由①可得
 ,
,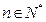 .
.所以对任意的
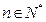 ,
,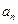 是
是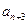 与
与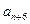 的等差中项.
的等差中项.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
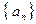 的前
的前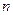 项和为
项和为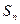 ,
,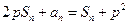
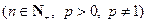 ,数列
,数列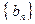 满足
满足 .(Ⅰ)求数列
.(Ⅰ)求数列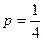 时,
时,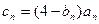 ,求数列
,求数列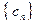 的前
的前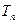 .
.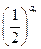 .已知b1+b2+b3=
.已知b1+b2+b3=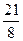 , b1b2b3=
, b1b2b3=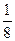 .求等差数列的通项an.
.求等差数列的通项an.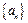 的前n项的和Sn,满足
的前n项的和Sn,满足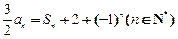 .
.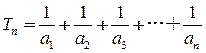 ,是否存在正整数k,使得当n≥3时,
,是否存在正整数k,使得当n≥3时,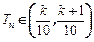 如果存在,求出k;如果不存在,请说明理由.
如果存在,求出k;如果不存在,请说明理由. 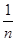 ),f(
),f(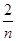 ),
),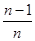 )……,(n≥2,n∈
)……,(n≥2,n∈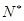 )的前n项的和为Sn ;
)的前n项的和为Sn ;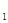 =
=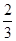 ,a
,a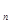 =" "
=" " 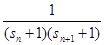 (n≥2,n∈
(n≥2,n∈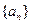 中,
中,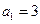 ,前
,前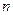 项和为
项和为 ,等比数列
,等比数列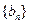 各项均为正数,
各项均为正数, ,且
,且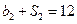 ,
,
 (1)求
(1)求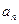 与
与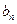 ;(2)证明:
;(2)证明: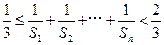
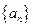 是等差数列,若
是等差数列,若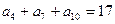 ,
,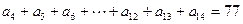 且
且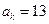 ,则
,则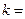 ___
___ 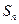 是等差数列
是等差数列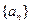 的前
的前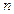 项和,若
项和,若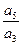 =
=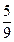 ,则
,则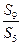 等于
等于