题目内容
设{an}是等差数列,bn=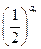 .已知b1+b2+b3=
.已知b1+b2+b3=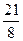 , b1b2b3=
, b1b2b3=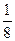 .求等差数列的通项an.
.求等差数列的通项an.
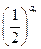 .已知b1+b2+b3=
.已知b1+b2+b3=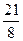 , b1b2b3=
, b1b2b3=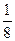 .求等差数列的通项an.
.求等差数列的通项an.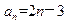 或
或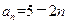 .
.本小题考查等差数列,等比数列的概念及运用方程(组)解决问题的能力.满分10分.
解 设等差数列{an}的公差为d,则an=a1+(n-1)d.
∴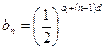 ,b1b3=
,b1b3=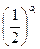 ·
· =
= =
=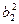 .
.
由b1b2b3=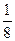 ,得
,得 =
=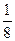 ,解得b2=
,解得b2=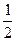 . ——3分
. ——3分
代入已知条件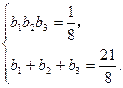 整理得
整理得
解这个方程组得b1=2,b3=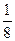 或b1=
或b1=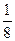 ,b3="2 " ——6分
,b3="2 " ——6分
∴a1=-1,d=2或a1=3,d=-2. ——8分
所以,当a1=-1,d=2时 an=a1+(n-1)d=2n-3.
当a1=3,d=-2时,an=a1+(n-1)d=5-2n. ——10分
解 设等差数列{an}的公差为d,则an=a1+(n-1)d.
∴
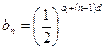 ,b1b3=
,b1b3=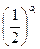 ·
· =
= =
=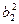 .
.由b1b2b3=
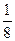 ,得
,得 =
=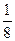 ,解得b2=
,解得b2=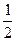 . ——3分
. ——3分代入已知条件
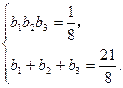 整理得
整理得
解这个方程组得b1=2,b3=
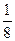 或b1=
或b1=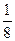 ,b3="2 " ——6分
,b3="2 " ——6分∴a1=-1,d=2或a1=3,d=-2. ——8分
所以,当a1=-1,d=2时 an=a1+(n-1)d=2n-3.
当a1=3,d=-2时,an=a1+(n-1)d=5-2n. ——10分

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
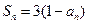 ,数列
,数列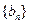 满足:
满足: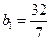 ,
,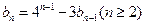
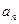 ;
;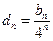 ,求
,求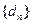 的通项公式;
的通项公式;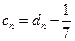 ,求
,求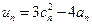 的最小值.
的最小值.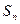 为等差数列
为等差数列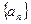 的前n项和,
的前n项和,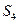 =14,S10-
=14,S10-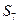 =30,则S9= .
=30,则S9= .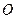 为
为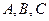 三点所在直线外一点,且
三点所在直线外一点,且 .数列
.数列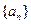 ,
,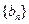 满足
满足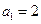 ,
,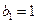 ,且
,且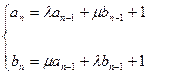 (
(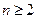 ).(Ⅰ) 求
).(Ⅰ) 求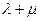 ;(Ⅱ) 令
;(Ⅱ) 令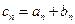 ,求数列
,求数列 的通项公式;(III) 当
的通项公式;(III) 当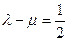 时,求数列
时,求数列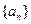 的前
的前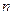 项和为
项和为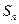 ,且
,且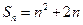 .数列
.数列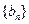 中,
中,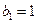 ,
,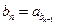
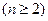 .(1)求数列
.(1)求数列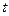 使数列
使数列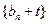 是等比数列,求数列
是等比数列,求数列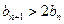 ;②
;②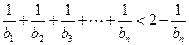 .
.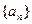 满足
满足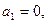
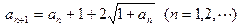 ,则
,则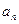 =___ .
=___ .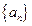 中,
中,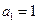 ,
,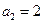 ,且
,且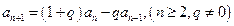 ;
;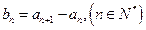 ,证明
,证明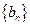 是等比数列;(2)求数列
是等比数列;(2)求数列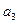 是
是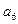 与
与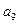 的等差中项,求
的等差中项,求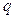 的值,并证明:对任意的
的值,并证明:对任意的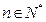 ,
,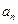 是
是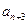 与
与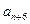 的等差中项;
的等差中项;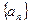 中,公差
中,公差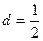 ,前
,前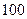 项的和
项的和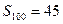 ,
,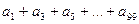 =_____________
=_____________