��Ŀ����
����Ŀ�����϶�������������ܶ�ѧУ����Ԫ���ż�ʱ�䣬��ǰ�ż���ѧ�����ڼҶ�����֣���и��ݡ�֣�������������칫�����ڽ�����Ⱦ������ɫԤ������Ϊ��ɫԤ����֪ͨ������12��29��12ʱ����ɫԤ������Ϊ��ɫԤ����12��30��0ʱ��������Ӧ����ȷҪ��������Сѧ�Ƚ�������ͣ�Σ�ͣ�β�ͣѧ����ѧ���ͼҳ���ͣ����һ�ٴ���һ����Ϊ�˽����ɵģ����µ���ѧϰ���ɵģ�ij�������Ϊ���˽�ڶԸþٴ��̬�ȣ��������ɷ���50�ˣ�����������������ܳ������
���䣨�꣩ | [15��25�� | [25��35�� | [35��45�� | [45��55�� | [55��65�� | [65��75] |
Ƶ�� | 5 | 10 | 15 | 10 | 5 | 5 |
������ | 4 | 6 | 9 | 6 | 3 | 4 |

��������ͼ����ɱ�������Ա�����Ƶ�ʷֲ�ֱ��ͼ��
��������������[25��35����[65��75]����ɷö����и����ѡȡ2�˽�����ȸ��ٵ��飬ѡ��4���в�������ٴ������ΪX�����������X�ķֲ��к���ѧ������
���𰸡��⣺������Ƶ���ֲ���֪�� ������[35��45����Ƶ��Ϊ�� ![]() =0.3����Ӧ��С�����и�Ϊ
=0.3����Ӧ��С�����и�Ϊ ![]() =0.03��
=0.03��
��ȫƵ�ʷֲ�ֱ��ͼ��ͼ��ʾ��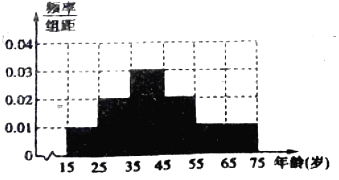
����X�����п��ܵ�ȡֵΪ0��1��2��3��![]() =
= ![]() ��
��![]() ��
��![]() ��
��![]() =
= ![]() ��
��
��X�ķֲ���Ϊ��
X | 0 | 1 | 2 | 3 |
P | | | | |
����X����ѧ����Ϊ ![]() ��
��
��������������Ƶ���ֲ������������[35��45����Ƶ�ʣ��Ӷ������Ӧ��С���εĸߣ��ɴ��ܲ�ȫƵ�ʷֲ�ֱ��ͼ������X�����п��ܵ�ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
�����㾫����������Ҫ��������ɢ�������������ֲ��е����֪ʶ�㣬��Ҫ�������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в�����ȷ�����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�