题目内容
19.设O为△ABC的外心(三角形外接圆的心),若$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|$\overrightarrow{AB}$|2,则$\frac{AC}{AB}$=( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 利用三角形的外心,得到$|\overrightarrow{AO}|=|\overrightarrow{BO}|=|\overrightarrow{CO|}$,$\overrightarrow{BO}=\overrightarrow{AO}-\overrightarrow{AB}$,$\overrightarrow{CO}=\overrightarrow{AO}-\overrightarrow{AC}$两式平方相减化简,得到2$\overrightarrow{AO}•\overrightarrow{CB}={\overrightarrow{AB}}^{2}-{\overrightarrow{AC}}^{2}$,又$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|$\overrightarrow{AB}$|2,得到AB,AC的关系
解答 解:因为O是三角形的外心,所以$|\overrightarrow{AO}|=|\overrightarrow{BO}|=|\overrightarrow{CO|}$,
$\overrightarrow{BO}=\overrightarrow{AO}-\overrightarrow{AB}$,$\overrightarrow{CO}=\overrightarrow{AO}-\overrightarrow{AC}$,两式平方相减得2$\overrightarrow{AO}•(\overrightarrow{AB}-\overrightarrow{AC})={\overrightarrow{AB}}^{2}-{\overrightarrow{AC}}^{2}$,即2$\overrightarrow{AO}•\overrightarrow{CB}={\overrightarrow{AB}}^{2}-{\overrightarrow{AC}}^{2}$,
又$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|$\overrightarrow{AB}$|2,所以2${\overrightarrow{AB}}^{2}={\overrightarrow{AC}}^{2}$,所以$\frac{AC}{AB}=\sqrt{2}$;
故选:B.
点评 本题考查了三角形外心性质以及向量数量积等运算;考查学生的运算能力;属于中档题.

| A. | (2,+∞) | B. | (-∞,-2) | C. | [2,+∞) | D. | (-∞,-2] |
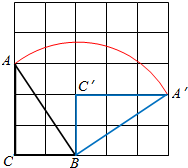 如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位.
如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是$\frac{13}{4}π$平方单位.