题目内容
2.若函数$f(x)=\left\{{\begin{array}{l}{{x^2}+(3-a)x+1,x≥0}\\{(a-1)x+2a-4,x<0}\end{array}}\right.$在R上为增函数,则a的取值范围为( )| A. | 1<a | B. | 1<a≤3 | C. | 1<a≤$\frac{5}{2}$ | D. | a≥3 |
分析 由题意可得$\frac{a-3}{2}$≤0,a-1>0,且1≥2a-4,由此求得a的范围.
解答 解:根据函数$f(x)=\left\{{\begin{array}{l}{{x^2}+(3-a)x+1,x≥0}\\{(a-1)x+2a-4,x<0}\end{array}}\right.$在R上为增函数,可得$\frac{a-3}{2}$≤0,a-1>0,且1≥2a-4,
求得1<a≤$\frac{5}{2}$,
故选:C.
点评 本题主要考查函数的单调性的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
11.已知集合M={x|0<x<1},N={x|x=t2+2t+3},则(∁NM)∩N=( )
| A. | {x|0<x<1} | B. | {x|x>1} | C. | {x|x≥2} | D. | {x|1<x<2} |
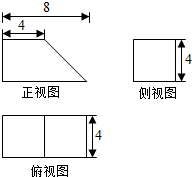 已知某几何体的三视图如下,请画出它的直观图(单位:cm)
已知某几何体的三视图如下,请画出它的直观图(单位:cm)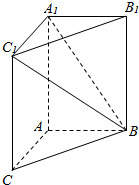 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.