题目内容
若正项数列 满足条件:存在正整数
满足条件:存在正整数 ,使得
,使得 对一切
对一切 都成立,则称数列
都成立,则称数列 为
为 级等比数列.
级等比数列.
(1)已知数列 为2级等比数列,且前四项分别为
为2级等比数列,且前四项分别为 ,求
,求 的值;
的值;
(2)若 为常数),且
为常数),且 是
是 级等比数列,求
级等比数列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值时数列
取最小正值时数列 的前
的前 项和
项和 ;
;
(3)证明: 为等比数列的充要条件是
为等比数列的充要条件是 既为
既为 级等比数列,
级等比数列, 也为
也为 级等比数列.
级等比数列.
 满足条件:存在正整数
满足条件:存在正整数 ,使得
,使得 对一切
对一切 都成立,则称数列
都成立,则称数列 为
为 级等比数列.
级等比数列.(1)已知数列
 为2级等比数列,且前四项分别为
为2级等比数列,且前四项分别为 ,求
,求 的值;
的值;(2)若
 为常数),且
为常数),且 是
是 级等比数列,求
级等比数列,求 所有可能值的集合,并求
所有可能值的集合,并求 取最小正值时数列
取最小正值时数列 的前
的前 项和
项和 ;
;(3)证明:
 为等比数列的充要条件是
为等比数列的充要条件是 既为
既为 级等比数列,
级等比数列, 也为
也为 级等比数列.
级等比数列.(1)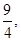 (2)
(2)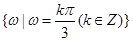 ,0,(3)详见解析.
,0,(3)详见解析.
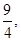 (2)
(2)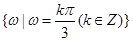 ,0,(3)详见解析.
,0,(3)详见解析.试题分析:(1)解新定义数列问题,关键从定义出发,建立等量关系.
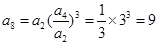 ,
,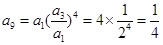 ,
,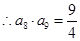 ,(2)本题化简是关键.因为
,(2)本题化简是关键.因为 是
是 级等比数列,所以
级等比数列,所以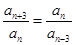
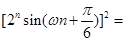
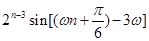
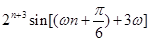
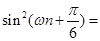
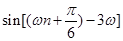

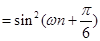
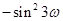
所以
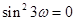 ,
,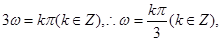
 最小正值等于
最小正值等于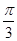 ,此时
,此时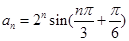
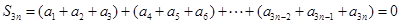 ,(3)充分性就是验证,易证,关键在于证必要性,可从两者中在交集(共同元素)出发.
,(3)充分性就是验证,易证,关键在于证必要性,可从两者中在交集(共同元素)出发. 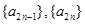 ,
, 成等比数列, 因此
成等比数列, 因此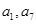 既是
既是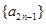 中的项,也是
中的项,也是 中的项,
中的项,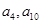 既是
既是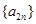 中的项,也是中
中的项,也是中 的项,可得它们公比的关系,进而推出三者结构统一,得出等比数列的结论.
的项,可得它们公比的关系,进而推出三者结构统一,得出等比数列的结论.解(1)
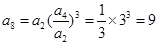 (2分)
(2分)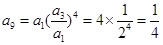
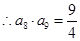 (4分)
(4分)(2)
 是
是 级等比数列,
级等比数列,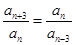
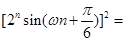
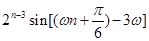
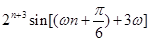 (1分)
(1分)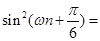
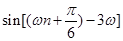

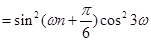

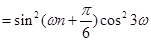

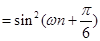
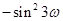
所以
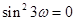 ,
,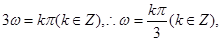
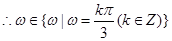 (3分)
(3分) 最小正值等于
最小正值等于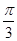 ,此时
,此时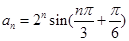
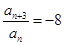 ,
,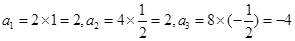 ,
,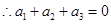
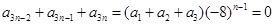 (5分)
(5分)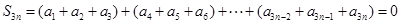 (6分)
(6分)(3)充分性:若
 为等比数列,则
为等比数列,则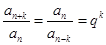
对一切
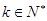 成立,显然对
成立,显然对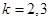 成立。
成立。所以
 既为
既为 级等比数列,
级等比数列, 也为
也为 级等比数列。 (2分)
级等比数列。 (2分)必要性:若
 为
为 级等比数列,
级等比数列,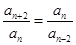 ,则
,则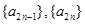 均成等比数列,设等比数列
均成等比数列,设等比数列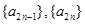 的公比分别为
的公比分别为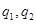 ,
, 为
为 级等比数列,
级等比数列,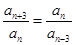 ,则
,则 成等比数列,设公比为
成等比数列,设公比为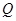 (3分)
(3分)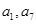 既是中
既是中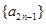 的项,也是
的项,也是 中的项,
中的项,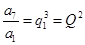
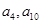 既是中
既是中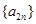 的项,也是中
的项,也是中 的项,
的项,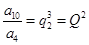
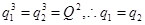 (5分)
(5分)设
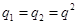 ,则
,则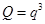
所以
 (
(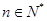 ),
),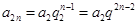 (
(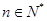 ),
),又
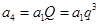 ,
,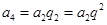 ,
,所以
 , (7分)
, (7分)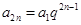 (
(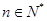 )
)所以,
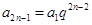 ,
,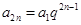 (
(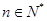 )
)综合得:
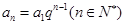 ,显然
,显然 为等比数列。 (8分)
为等比数列。 (8分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
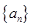 满足
满足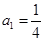 ,
,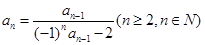 .
.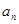 ;
;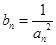 ,求数列
,求数列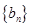 的前n项和
的前n项和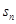 ;
;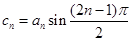 ,数列
,数列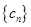 的前n项和为
的前n项和为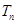 .求证:对任意的
.求证:对任意的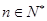 ,
,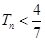 .
.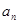 }中,
}中,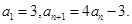
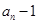 }是等比数列,并求出数列{
}是等比数列,并求出数列{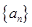 的前
的前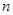 项和为
项和为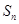 ,且
,且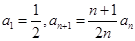 .
.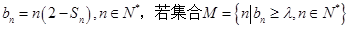 恰有5个元素,求实数
恰有5个元素,求实数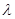 的取值范围.
的取值范围. 的前n项和为
的前n项和为 ,已知
,已知 成等差数列,则数列
成等差数列,则数列