题目内容
【题目】已知函数![]() (
(![]() ,
,![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 在
在![]() 上有两个零点,求
上有两个零点,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,是否存在
时,是否存在![]() ,使得不等式
,使得不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
【答案】(1)![]() .(2)存在,
.(2)存在,![]() 的取值集合为
的取值集合为![]() .
.
【解析】
(1)将![]() 代入,求得函数的导数,当
代入,求得函数的导数,当![]() 时显然不成立,当
时显然不成立,当![]() 时,利用零点的存在定理,即可求解的结论;
时,利用零点的存在定理,即可求解的结论;
(2)当![]() 时,设
时,设![]() ,由
,由![]() ,进而条件转化为不等式
,进而条件转化为不等式![]() 对
对![]() 恒成立,得到
恒成立,得到![]() 是函数
是函数![]() 的最大值,也是函数
的最大值,也是函数![]() 的极大值,故
的极大值,故![]() ,当
,当![]() 时,利用导数得到不等式
时,利用导数得到不等式![]() 恒成立,即可求解.
恒成立,即可求解.
(1)当![]() 时,
时,![]() ,
,![]() (
(![]() ),
),
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,不合题意,舍去;
上单调递增,不合题意,舍去;
当![]() 时,
时,![]() ,
,![]() ,
,
进而![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
依题意有![]() ,
,![]() ,
,![]() ,解得
,解得![]() ,
,
又![]() ,且
,且![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
进而由零点存在定理可知,函数![]() 在
在![]() 上存在唯一零点;
上存在唯一零点;
下面先证![]() (
(![]() )恒成立,令
)恒成立,令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
进而![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
可得![]() ,
,
若![]() ,得
,得![]() ,
,
因为![]() ,则
,则![]() ,即当
,即当![]() 时,取
时,取![]() ,有
,有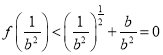 ,
,
即存在![]() 使得
使得![]() ,
,
进而由零点存在定理可知![]() 在
在![]() 上存在唯一零点;
上存在唯一零点;
(2)当![]() 时,存在
时,存在![]() ,使得不等式
,使得不等式![]() 恒成立.
恒成立.
证明如下:
当![]() 时,设
时,设![]() ,则
,则![]() ,
,
依题意,函数![]() 恒成立,
恒成立,
又由![]() ,进而条件转化为不等式
,进而条件转化为不等式![]() 对
对![]() 恒成立,
恒成立,
所以![]() 是函数
是函数![]() 的最大值,也是函数
的最大值,也是函数![]() 的极大值,故
的极大值,故![]() ,解得
,解得![]() .
.
当![]() 时,
时,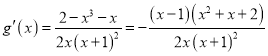 (
(![]() ),
),
令![]() 可得
可得![]() ,令
,令![]() 可得
可得![]() .
.
故![]() 在
在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
因此![]() ,即不等式
,即不等式![]() 恒成立.
恒成立.
综上,存在且![]() 的取值集合为
的取值集合为![]() .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】为了判断英语词汇量与阅读水平是否相互独立,某语言培训机构随机抽取了100位英语学习者进行调查,经过计算![]() 的观测值为7,根据这一数据分析,下列说法正确的是( )
的观测值为7,根据这一数据分析,下列说法正确的是( )
附:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
A.有99%以上的把握认为英语词汇量与阅读水平无关
B.有99.5%以上的把握认为英语词汇量与阅读水平有关
C.有99.9%以上的把握认为英语词汇量与阅读水平有关
D.在犯错误的概率不超过1%的前提下,可以认为英语词汇量与阅读水平有关