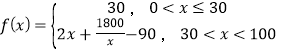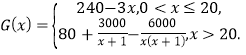Question

【题目】在平面直角坐标系xOy中，曲线C的参数方程为，（θ为参数），以原点为极点，x轴非负半轴为极轴建立极坐标系．

（1）求曲线C的极坐标方程；

（2）在平面直角坐标系xOy中，A（﹣2，0），B（0，﹣2），M是曲线C上任意一点，求△ABM面积的最小值．

Answer 1

【答案】（1）ρ2﹣6ρcosθ﹣8ρsinθ+21＝0．（2）9﹣2．

【解析】

(1)先将化简成直角坐标方程,再利用与化简即可.

(2)由为以为底,到的距离为高可知要求面积的最小值即求到的距离最大值.再设求解最值即可.

（1）∵曲线C的参数方程为,（θ为参数）,有.

上下平方相加得曲线C的直角坐标方程为,

化简得

将与,代入得曲线C的直角坐标方程有：

．

（2）设点到直线AB：x+y+2＝0的距离为d,

则,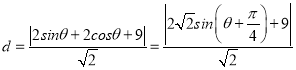

当sin（）＝﹣1时,d有最小值,

所以△ABM面积的最小值S9﹣2．