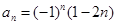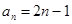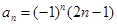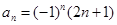题目内容
设项数均为k(k≥2,k∈N*)的数列{an}、{bn}、{cn}前n项的和分别为Sn、Tn、Un.已知:an-bn=2n(1≤n≤k,n∈N*),且集合{a1,a2,…,ak,b1,b2,…,bk}={2,4,6,…,4k-2,4k}.
(1)已知Un=2n+2n,求数列{cn}的通项公式;
(2)若k=4,求S4和T4的值,并写出两对符合题意的数列{an}、{bn};
(3)对于固定的k,求证:符合条件的数列对({an},{bn})有偶数对.
(1)已知Un=2n+2n,求数列{cn}的通项公式;
(2)若k=4,求S4和T4的值,并写出两对符合题意的数列{an}、{bn};
(3)对于固定的k,求证:符合条件的数列对({an},{bn})有偶数对.
(1)n=1时,c1=U1=4,
当n≥2时,cn=Un-Un-1=2n+2n-2(n-1)-2n-1=2+2n-1,
c1=4不适合该式,
故cn=
,
(2)S4-T4=(a1+a2+a3+a4)-(b1+b2+b3+b4)
=(a1-b1)+(a2-b2)+(a3-b3)+(a4-b4)
=2+4+6+8=20,
又S4+T4=(a1+a2+a3+a4)+(b1+b2+b3+b4)
=2+4+6+8+10+12+14+16
=72,
∴S4=46,T4=26;
数列{an}、{bn}可以为:
①16,10,8,12;14,6,2,4②14,6,10,16;12,2,4,8
③6,16,14,10;4,12,8,2④4,14,12,16;2,10,6,8
⑤4,12,16,14;2,8,10,6⑥16,8,12,10;14,4,6,2;
(3)令dn=4k+2-bn,en=4k+2-an(1≤n≤k,n∈N*),
dn-en=(4k+2-bn)-(4k+2-an)=an-bn=2n;
又{a1,a2,…,ak,b1,b2,…,bk}={2,4,6,…,4k},
得{4k+2-a1,4k+2-a2,…,4k+2-ak,4k+2-b1,4k+2-b2,…,4k+2-bk}
={2,4,6,…,4k};
∴数列对({an},{bn})与({dn},{en})成对出现.
假设数列{an}与{dn}相同,则由d2=4k+2-b2=a2及a2-b2=4,得a2=2k+3,b2=2k-1,均为奇数,矛盾!
故符合条件的数列对({an},{bn})有偶数对.
当n≥2时,cn=Un-Un-1=2n+2n-2(n-1)-2n-1=2+2n-1,
c1=4不适合该式,
故cn=
|
(2)S4-T4=(a1+a2+a3+a4)-(b1+b2+b3+b4)
=(a1-b1)+(a2-b2)+(a3-b3)+(a4-b4)
=2+4+6+8=20,
又S4+T4=(a1+a2+a3+a4)+(b1+b2+b3+b4)
=2+4+6+8+10+12+14+16
=72,
∴S4=46,T4=26;
数列{an}、{bn}可以为:
①16,10,8,12;14,6,2,4②14,6,10,16;12,2,4,8
③6,16,14,10;4,12,8,2④4,14,12,16;2,10,6,8
⑤4,12,16,14;2,8,10,6⑥16,8,12,10;14,4,6,2;
(3)令dn=4k+2-bn,en=4k+2-an(1≤n≤k,n∈N*),
dn-en=(4k+2-bn)-(4k+2-an)=an-bn=2n;
又{a1,a2,…,ak,b1,b2,…,bk}={2,4,6,…,4k},
得{4k+2-a1,4k+2-a2,…,4k+2-ak,4k+2-b1,4k+2-b2,…,4k+2-bk}
={2,4,6,…,4k};
∴数列对({an},{bn})与({dn},{en})成对出现.
假设数列{an}与{dn}相同,则由d2=4k+2-b2=a2及a2-b2=4,得a2=2k+3,b2=2k-1,均为奇数,矛盾!
故符合条件的数列对({an},{bn})有偶数对.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ……的一个通项公式为( )
……的一个通项公式为( )