题目内容
如图所示,将数以斜线作如下分群:(1),(2,3),(4,6,5),(8,12,10,7),(16,24,20,14,9),….并顺次称其为第1群,第2群,第3群,第4群,….则第7群中的第2项是:______;
第n群中n个数的和是:______.
| 1 | 3 | 5 | 7 | 9 | … |
| 2 | 6 | 10 | 14 | 18 | … |
| 4 | 12 | 20 | 28 | 36 | … |
| 8 | 24 | 40 | 56 | 72 | … |
| 16 | 48 | 80 | 112 | 114 | … |
| … | … | … | … | … | … |
由题意数列可以转化为:
1
2 3
4 6 5
8 1210 7
16 2420 14 9
32 4840 2819 11
…
类似杨辉三角,可知每一列都是等比数列,每一行最后一个数是等差数列,公差为2,
所以第7群中的第2项是:3×25=96.
第n个群中n个数为:Sn=1×2 n-1+3×2n-2+5×2 n-3+…+(2n-1)•2 0…①
2Sn=1×2 n+3×2n-1+5×2 n-2+…+(2n-1)•2 1…②,
②-①得,Sn=2 n+2×2n-1+2×2 n-2+…+2•2 1-2n+1
=2 n+2n+2 n-1+…+2 2-2n+1
=2 n+
-2n+1
=3•2n-2n-3.
故答案为:96;3•2n-2n-3.
1
2 3
4 6 5
8 1210 7
16 2420 14 9
32 4840 2819 11
…
类似杨辉三角,可知每一列都是等比数列,每一行最后一个数是等差数列,公差为2,
所以第7群中的第2项是:3×25=96.
第n个群中n个数为:Sn=1×2 n-1+3×2n-2+5×2 n-3+…+(2n-1)•2 0…①
2Sn=1×2 n+3×2n-1+5×2 n-2+…+(2n-1)•2 1…②,
②-①得,Sn=2 n+2×2n-1+2×2 n-2+…+2•2 1-2n+1
=2 n+2n+2 n-1+…+2 2-2n+1
=2 n+
| 4(1-2n-1) |
| 1-2 |
=3•2n-2n-3.
故答案为:96;3•2n-2n-3.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目

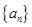 为等差数列,且
为等差数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,
, 且
且 .
. ,
, 为数列
为数列 的前
的前 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.