题目内容
【题目】如图所示为一名曰“堑堵”的几何体，已知 AE⊥底面BCFE ， DF ∥ AE ， DF = AE = 1， CE =
，四边形ABCD 是正方形．
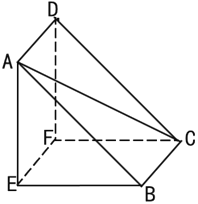
（1）《九章算术》中将四个面都是直角三角形的四面体称为鳖臑．判断四面体 EABC 是否为鳖臑，若是，写出其 每一个面的直角，并证明；若不是，请说明理由．
（2）求四面体 EABC 的体积．
【答案】（1）是，详见解析 （2） 
【解析】
（1）推导出
，
，
，从而
，再上
面
，知
，从而得到四面体
是鳖臑．
（2）
是三棱锥
的高，求出正方形
的边长，由此能求出四面体的体积．
解：（1）
底面
，
，
，
都在底面上，
，，，
四边形是正方形有，
，
面
，又
面，
，
四面体是鳖臑．
（2）由（1）得是三棱锥的高，
设正方形的边长为
，则
，
，
，
在
中，
，
即
，解得
，
，
四面体的体积
．
练习册系列答案
相关题目
