题目内容
【题目】设函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,求证:
时,求证:![]() 有且仅有一个零点;
有且仅有一个零点;
(2)若函数![]() 在定义域内既有极大值,又有极小值,求
在定义域内既有极大值,又有极小值,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)利用导数求出函数的单调性和极值,结合极值的大小即可证出![]() 有且仅有一个零点;
有且仅有一个零点;
(2)因为函数![]() 在定义域内既有极大值,又有极小值,所以
在定义域内既有极大值,又有极小值,所以![]() 有两个正根,再利用根与系数的关系即可求出
有两个正根,再利用根与系数的关系即可求出![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]() ,
,![]() ,
,
解![]() ,得
,得![]() ,
,![]() ,
,
列表如下:
|
| 1 |
| 2 |
|
| + | 0 | ﹣ | 0 | + |
|
| 极大值 |
| 极小值 |
|
因为极大值![]() ,所以
,所以![]() 在
在![]() 无零点,从而在
无零点,从而在![]() 无零点,
无零点,
又因为![]() ,
,![]() ,所以
,所以![]() 在
在![]() 有零点,因为
有零点,因为![]() 在
在![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 有唯一零点,即
有唯一零点,即![]() 有且仅有一个零点;
有且仅有一个零点;
(2)![]() ,
,
∵函数![]() 在定义域内既有极大值,又有极小值,∴
在定义域内既有极大值,又有极小值,∴![]() 有两个正根,
有两个正根,
即![]() 有两个正根
有两个正根![]() 、
、![]() ,
,
所以,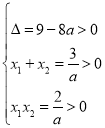 ,
,
解得![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
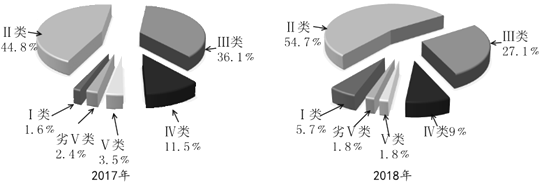
【题目】每年的4月23日为“世界读书日”,某调查机构对某校学生做了一个是否喜爱阅读的抽样调查.该调查机构从该校随机抽查了100名不同性别的学生(其中男生45名),统计了每个学生一个月的阅读时间,其阅读时间![]() (小时)的频率分布直方图如图所示:
(小时)的频率分布直方图如图所示:
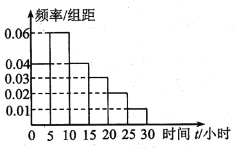
(1)求样本学生一个月阅读时间![]() 的中位数
的中位数![]() .
.
(2)已知样本中阅读时间低于![]() 的女生有30名,请根据题目信息完成下面的
的女生有30名,请根据题目信息完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
![]() 列联表
列联表
男 | 女 | 总计 | |
| |||
| |||
总计 |
附表:
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
其中: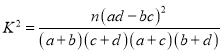 .
.
【题目】已知某产品的销售额![]() 与广告费用
与广告费用![]() 之间的关系如下表:
之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得![]() 对
对![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.产品的销售额与广告费用成正相关
B.该回归直线过点![]()
C.当广告费用为10万元时,销售额一定为74万元
D.![]() 的值是20
的值是20