题目内容
5.用|S|表示集合S的元素个数,由n个集合为元素组成的集合称为“n个元素”,如果集合A、B、C满足、|A∩B|=|B∩C|=|A∩C|=1,且A∩B∩C=∅,则称{A,B,C}为最小相交“三元集”.给出下列命题:①集合{1,2}的非空子集能组成6个“二元集”;
②若集合M的子集构成的“三元集”存在最小相交“三元集”,则|M|≥3;
③集合{1,2,3,4}的子集构成所有“三元集”中,最小相交“三元集”共有16个;
④若集合|M|=n,则它的子集构成所有“三元集”中,最小相交“三元集”共有2n个.
其中正确的命题有②③.(请填上你认为所有正确的命题序号)
分析 对于①,集合{1,2}的非空子集个数为3,列举即可判断;
对于②,考虑集合M的子集构成的“三元集”存在最小相交“三元集”,且|M|<3,讨论|M|=1,|M|=2不成立;
对于③,设A∩B={x},B∩C={y},C∩A={z},∵A∩B∩C=∅,且x,y,z∈{1,2,3,4},讨论A,B,C中元素个数,即可判断;
对于④,若集合|M|=n,若n=5,讨论满足条件的三元集的个数,即可判断.
解答 解:对于①,集合{1,2}的非空子集个数为3,且为{1},{2},{1,2},能组成3个“二元集”,则①错误;
对于②,若集合M的子集构成的“三元集”存在最小相交“三元集”,且|M|<3,则|M|=1显然不成立,
当|M|=2,共有3个非空子集,A,B,C不满足|A∩B|=|B∩C|=|A∩C|=1,但满足A∩B∩C=∅,
则|M|=2不成立,则②正确;
对于③,∵|A∩B|=|B∩C|=|C∩A|=1,∴设A∩B={x},B∩C={y},C∩A={z},
∵A∩B∩C=∅,且x,y,z∈{1,2,3,4},∴若集合{1,2,3,4}中的子集含有4个元素时,
∴从1,2,3,4四个元素选3个有${C}_{4}^{3}$=4种方法,剩余的一个元素可以分别放入集合A,B,C,有3种,
∴此时共有3×4=12种.
若集合{1,2,3,4}中的子集含有3个元素时,满足集合A,B,C中都只有一个元素.
∴从1,2,3,4四个元素选3个有${C}_{4}^{3}$=4种方法,
综上共有12+4=16个.则③正确;
对于④,若集合|M|=n,若n=5,∵|A∩B|=|B∩C|=|C∩A|=1,∴设A∩B={x},B∩C={y},C∩A={z},
∵A∩B∩C=∅,且x,y,z∈{1,2,3,4,5},
∴若集合{1,2,3,4,5}中的子集含有5个元素时,
∴从1,2,3,4,5五个元素选4个有${C}_{5}^{4}$=5种方法,剩余的一个元素可以分别放入集合A,B,C,有3种,
∴此时共有3×5=15种.
若集合{1,2,3,4,5}中的子集含有4个元素时,从1,2,3,4,5五个元素选3个有${C}_{5}^{3}$=10种方法,剩余的一个元素可以分别放入集合A,B,C,有3种,∴此时共有3×10=30种.
若集合{1,2,3,4,5}中的子集含有3个元素时,满足集合A,B,C中都只有一个元素.
∴从1,2,3,4,5五个元素选3个有${C}_{5}^{3}$=10种方法,
综上共有15+30+10=55个.则④错误.
故答案为:②③.
点评 本题主要考查集合的关系的应用,正确理解新定义是解决本题关键,利用排列组合的知识是解决本题的突破点.

| A. | ($\sqrt{2}$-1)2 | B. | 2($\sqrt{2}$+1)2 | C. | 3($\sqrt{2}$-1)2 | D. | 4($\sqrt{2}$+1)2 |
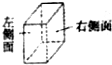 如图所示的长方体,将其左侧面作为上底面,右侧面作为下底面,水平放置,所得的几何体是( )
如图所示的长方体,将其左侧面作为上底面,右侧面作为下底面,水平放置,所得的几何体是( )| A. | 棱柱 | B. | 棱台 | ||
| C. | 棱柱与棱锥组合体 | D. | 无法确定 |