题目内容
9.在满足面积和周长的数值相等的所有直角三角形中,面积的最小值为( )| A. | ($\sqrt{2}$-1)2 | B. | 2($\sqrt{2}$+1)2 | C. | 3($\sqrt{2}$-1)2 | D. | 4($\sqrt{2}$+1)2 |
分析 设直角三角形直角边长为a、b,则由题意可得$\frac{ab}{2}$=a+b+$\sqrt{{a}^{2}{+b}^{2}}$,再利用基本不等式求得三角形的面积$\frac{1}{2}$ab的最小值.
解答 解:设直角三角形直角边长为a、b,则由题意可得$\frac{ab}{2}$=a+b+$\sqrt{{a}^{2}{+b}^{2}}$≥2$\sqrt{ab}$+$\sqrt{2ab}$,
即 ab≥4$\sqrt{ab}$+2$\sqrt{2}$•$\sqrt{ab}$,求得$\sqrt{ab}$≥4+2$\sqrt{2}$,∴$\frac{1}{2}$ab≥4($\sqrt{2}$+1)2,
当且仅当a=b=4+2$\sqrt{2}$时,取等号,
故面积的最小值为4($\sqrt{2}$+1)2,
故选:D.
点评 本题主要考查勾股定理、基本不等式的应用,注意等号成立条件,属于基础题.

练习册系列答案
相关题目
8.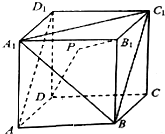 如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
 如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )| A. | [0,$\frac{1}{2}$] | B. | [0,$\frac{1}{3}$] | C. | [$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |