Question

【题目】在四棱锥P-ABCD中，底面ABCD是梯形，AB∥DC，AD⊥DC，AB=AD=2，DC=3，平面PDC⊥平面ABCD，E在棱PC上且PE=2EC。

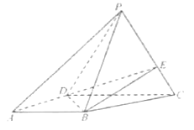
()证明：BE∥平面PAD；

(1)若ΔPDC是正三角形，求三棱锥P-DBE的体积。

Answer 1

【答案】(1) 见证明；(2)

【解析】

(1) 作EF∥DC交PD于点F，连接AF，利用PE=2EC可得FE=2，再利用AB∥DC即可证得四边形ABEF为平行四边形，问题得证。

(2)利用平面PDC⊥平面ABCD及AD⊥DC即可证得：AD⊥平面PDC，利用体积转化可得：，再利用锥体体积计算公式即可得解。

(1)证明：作EF∥DC交PD于点F，连接AF，

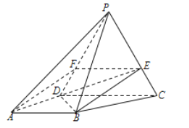
因为E在棱PC上且PE=2EC，

所以FE=DC=2，

又因为AB∥DC，AB=2，

所以AB∥FE，且AB=FE，

所以四边形ABEF为平行四边形，

从而有AF∥BE

又因为BE平面PAD，AF平面PAD，

所以BE∥平面PAD

(2)因为平面PDC⊥平面ABCD，且交线为DC，AD⊥DC，AD平面ABCD

所以AD⊥平面PDC.

因为PE=2EC

所以

即三棱锥P-DBE的体积为。