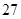题目内容
已知实数 ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求实数 的值;
的值;
(2)若等差数列 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列 的首项和公比都为
的首项和公比都为 ,数列
,数列 和
和 的前
的前 项和分别为
项和分别为 ,且
,且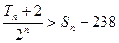 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.
 ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.(1)求实数
 的值;
的值;(2)若等差数列
 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列 的首项和公比都为
的首项和公比都为 ,数列
,数列 和
和 的前
的前 项和分别为
项和分别为 ,且
,且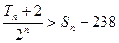 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.(1) (2)14
(2)14
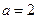 (2)14
(2)14(1)解法一:由已知三个数有: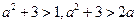 , 不妨设排列成递增的等差数列,则
, 不妨设排列成递增的等差数列,则
①若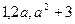 依次成等差数列,则有
依次成等差数列,则有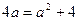 解得
解得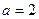 ,符合题意;
,符合题意;
②若 依次成等差数列,则有
依次成等差数列,则有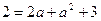 解得
解得 ,由
,由 不符合题意;
不符合题意;
综上得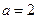 .
.
解法二:分三种情况讨论:
①若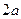 为等差中项,则有
为等差中项,则有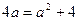 解得
解得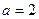 ,符合题意;
,符合题意;
②若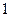 为等差中项,则有
为等差中项,则有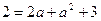 解得
解得 ,由
,由 不符合题意;
不符合题意;
③若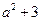 为等差中项,则有
为等差中项,则有 ,即
,即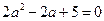 ,
, 方程无解;……6分
方程无解;……6分
综上得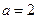 .(2)解:由(1)知
.(2)解:由(1)知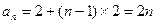 ,
,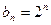 ,
,
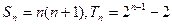 ,
,
由已知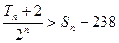 可得
可得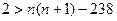 ,即
,即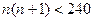 ,
,
即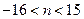 ,又
,又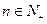 ,故
,故 的最大值为14.
的最大值为14.
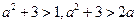 , 不妨设排列成递增的等差数列,则
, 不妨设排列成递增的等差数列,则①若
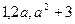 依次成等差数列,则有
依次成等差数列,则有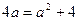 解得
解得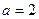 ,符合题意;
,符合题意;②若
 依次成等差数列,则有
依次成等差数列,则有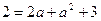 解得
解得 ,由
,由 不符合题意;
不符合题意;综上得
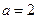 .
.解法二:分三种情况讨论:
①若
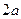 为等差中项,则有
为等差中项,则有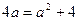 解得
解得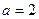 ,符合题意;
,符合题意;②若
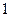 为等差中项,则有
为等差中项,则有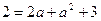 解得
解得 ,由
,由 不符合题意;
不符合题意;③若
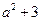 为等差中项,则有
为等差中项,则有 ,即
,即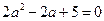 ,
, 方程无解;……6分
方程无解;……6分综上得
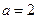 .(2)解:由(1)知
.(2)解:由(1)知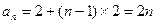 ,
,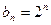 ,
,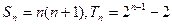 ,
,由已知
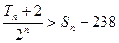 可得
可得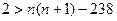 ,即
,即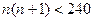 ,
,即
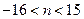 ,又
,又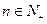 ,故
,故 的最大值为14.
的最大值为14.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 }是等比数列.
}是等比数列. 中,其前
中,其前 项和为
项和为 ,且
,且 .
. 是数列
是数列 的前
的前 是数列
是数列 的前
的前 .
.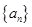 和
和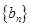 满足:
满足: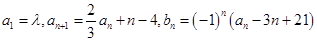 ,其中
,其中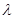 为实数,
为实数,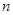 为正整数.
为正整数.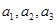 不成等比数列;
不成等比数列;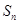 为数列
为数列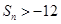 ?若存在,求
?若存在,求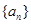 的各项均为正数,记
的各项均为正数,记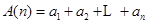 ,
,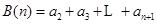 ,
, .
.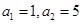 ,且对任意
,且对任意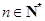 ,三个数
,三个数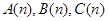 组成等差数列,求数列
组成等差数列,求数列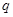 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意 ,前
,前 项的和为
项的和为 .
. ;
;
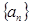 的前
的前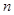 项和为
项和为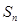 ,若
,若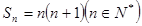 .则
.则 .
.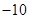 的等差数列,从第
的等差数列,从第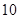 项起开始为正数,则公差
项起开始为正数,则公差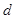 的取值范围是( ).
的取值范围是( ). 



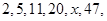 …中的
…中的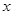 等于( )
等于( )