题目内容
【题目】已知正项等比数列{an}满足a1 , 2a2 , a3+6成等差数列,且a42=9a1a5 ,
(1)求数列{an}的通项公式;
(2)设bn=( ![]() an+1)an , 求数列{bn}的前n项和Tn .
an+1)an , 求数列{bn}的前n项和Tn .
【答案】
(1)解:设正项等比数列{an}的公比为q>0,∵a1,2a2,a3+6成等差数列,∴2×2a2=a3+6+a1,又a42=9a1a5,
∴ 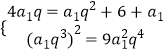 ,解得a1=q=3.
,解得a1=q=3.
∴an=3n.
(2)解:bn=( ![]() an+1)an=(2n+1)3n.
an+1)an=(2n+1)3n.
∴数列{bn}的前n项和Tn=3×3+5×32+…+(2n+1)3n.
3Tn=3×32+5×33+…+(2n﹣1)3n+(2n+1)3n+1,
∴﹣2Tn=32+2×(32+33+…+3n)﹣(2n+1)3n+1= ![]() +3﹣(2n+1)3n+1=﹣2n3n+1,
+3﹣(2n+1)3n+1=﹣2n3n+1,
∴Tn=n3n+1.
【解析】(1)利用等差数列与等比数列的通项公式即可得出.(2)bn=( ![]() an+1)an=(2n+1)3n . 再利用“错位相减法”与等比数列的前n项和公式即可得出.
an+1)an=(2n+1)3n . 再利用“错位相减法”与等比数列的前n项和公式即可得出.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系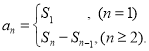 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 阅读快车系列答案
阅读快车系列答案【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人数 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:
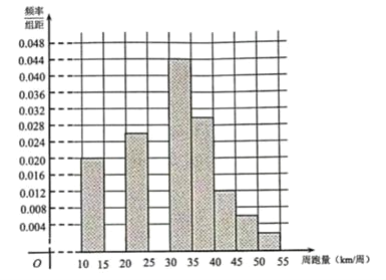
注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为![]() ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
类别 | 休闲跑者 | 核心跑者 | 精英跑者 |
装备价格(单位:元) | 2500 | 4000 | 4500 |
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?

