题目内容
【题目】如图,在平面直角坐标系![]() 中, 已知圆
中, 已知圆![]()
![]() ,椭圆
,椭圆![]()
![]() ,
,![]() 为椭圆右顶点.过原点
为椭圆右顶点.过原点![]() 且异于坐标轴的直线与椭圆
且异于坐标轴的直线与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,直线
,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,其中
,其中![]() .设直线
.设直线![]() 的斜率分别为
的斜率分别为![]() .
.

(1)求![]() 的值;
的值;
(2)记直线![]() 的斜率分别为
的斜率分别为![]() ,是否存在常数
,是否存在常数![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)求证:直线![]() 必过点
必过点![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)详见解析
(3)详见解析
【解析】
试题分析:(1)设![]() ,则
,则![]() ,代入椭圆方程,运用直线的斜率公式,化简即可得到所求值;(2)联立直线
,代入椭圆方程,运用直线的斜率公式,化简即可得到所求值;(2)联立直线![]() 的方程和圆方程,求得
的方程和圆方程,求得![]() 的坐标;联立直线
的坐标;联立直线![]() 的方程和椭圆方程,求得
的方程和椭圆方程,求得![]() 的坐标,再求直线
的坐标,再求直线![]() ,和直线
,和直线![]() 的斜率,即可得到结论;
的斜率,即可得到结论;
试题解析:(1)设![]() ,则
,则![]() ,
,![]()
所以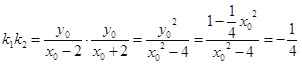
(2)联立![]() 得
得![]() ,
,
解得![]() ,
,
联立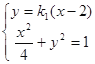 得
得![]() ,
,
解得![]() ,
,![]()
所以![]() ,
,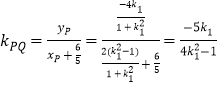 ,
,
所以![]() ,故存在常数
,故存在常数![]() ,使得
,使得![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目