题目内容
【题目】在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() .
.
(1)若![]() 为
为![]() 边的中点,求证:
边的中点,求证: ![]() ;
;
(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)详见解析;(2)1.
【解析】
(1)证法一:根据![]() 为
为![]() 边的中点,可以得到向量等式
边的中点,可以得到向量等式![]() ,平方,再结合余弦定理,可以证明出等式
,平方,再结合余弦定理,可以证明出等式![]() ;
;
证法二:分别在![]() 和
和![]() 中,利用余弦定理求出
中,利用余弦定理求出![]() 和
和![]() 的表达式,利用
的表达式,利用![]() ,可以证明出等式
,可以证明出等式![]() ;
;
(2)解法一:解法一:记![]() 面积为
面积为![]() .由题意并结合(1)
.由题意并结合(1)
所证结论得:![]() ,利用已知
,利用已知
![]() ,再结合基本不等式,最后求可求出
,再结合基本不等式,最后求可求出![]() 面积的最大值;
面积的最大值;
解法二:利用余弦定理把![]() 表示出来,结合重要不等式,再利用三角形面积公式可得
表示出来,结合重要不等式,再利用三角形面积公式可得
![]() ,令设
,令设![]() ,利用辅助角公式,可以求出
,利用辅助角公式,可以求出![]() 的最大值,即可求出
的最大值,即可求出![]() 面积的最大值.
面积的最大值.
(1)证法一:由题意得![]()
![]() ①
①
由余弦定理得![]() ②
②
将②代入①式并化简得![]() ,
,
故![]() ;
;
证法二:在![]() 中,由余弦定理得
中,由余弦定理得 ,
,
在![]() 中,由余弦定理得
中,由余弦定理得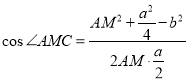 ,
,
∵![]() ,∴
,∴![]() ,
,
则![]() ,故
,故![]() ;
;
(2)解法一:记![]() 面积为
面积为![]() .由题意并结合(1)
.由题意并结合(1)
所证结论得:![]() ,
,
又已知![]() ,
,
则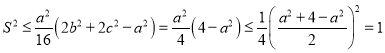 ,
,
即![]() ,当
,当![]() 时,等号成立,故
时,等号成立,故![]() ,
,
即![]() 面积的最大值为1.
面积的最大值为1.
解法二:![]()
![]()
设![]()
则![]()
由![]() ,
,
故![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某学校高中毕业班有男生900人,女生600人,学校为了对高三学生数学学习情况进行分析,从高三年级按照性别进行分层抽样,抽取200名学生成绩,统计数据如表所示:
分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
频数 | 20 | 40 | 70 | 50 | 20 | 200 |
(1)若成绩90分以上(含90分),则成绩为及格,请估计该校毕业班平均成绩及格学生人数;
(2)如果样本数据中,有60名女生数学成绩合格,请完成如下数学成绩与性别的列联表,并判断是否有90%的把握认为“该校学生的数学成绩与性别有关”.
女生 | 男生 | 总计 | |
及格人数 | 60 | ||
不及格人数 | |||
总计 |
参考公式:K2= ![]() .
.
P(K2≥k0) | 0.10 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
