题目内容
已知椭圆方程为 ,O为原点,F为右焦点,点M是椭圆右准线
,O为原点,F为右焦点,点M是椭圆右准线 上(除去与
上(除去与 轴的交点)的动点,过F作OM的垂线与以OM为直线的圆交于点N,则线段ON的长为 ( )
轴的交点)的动点,过F作OM的垂线与以OM为直线的圆交于点N,则线段ON的长为 ( )
 ,O为原点,F为右焦点,点M是椭圆右准线
,O为原点,F为右焦点,点M是椭圆右准线 上(除去与
上(除去与 轴的交点)的动点,过F作OM的垂线与以OM为直线的圆交于点N,则线段ON的长为 ( )
轴的交点)的动点,过F作OM的垂线与以OM为直线的圆交于点N,则线段ON的长为 ( )A. | B. | C. | D.不确定 |
C
分析:首先结合题意利用点斜式写出直线FN的方程,并且进行整理,设N(x,y),再由ON⊥NM,即斜率之积等于-1得到一个关于x,y的等式,进而把直线FN的方程代入此等式化简,可得x2+y2=a2,即可得到线段ON的长.
解:由题意可得设F(c,0),点M(
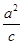 ,m),
,m),∴kOM=
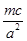 ,
,由题意可得:OM⊥FN,
∴FN的方程为:y-0=
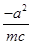 (x-c),
(x-c),∴整理方程可得:my=
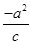 (x-c),即my+
(x-c),即my+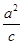 x=a2①,
x=a2①,∵过点F作OM的垂线与以OM为直径的圆交于点N,
∴ON⊥NM,即KON?KNM=-1,
设N(x,y),
∴
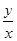 ?
?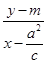 =-1,整理可得:x2+y2=
=-1,整理可得:x2+y2=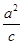 x+my ②,
x+my ②,联立①②得:x2+y2=
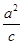 x+my=a2,
x+my=a2,∴|ON|=
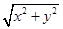 =a.
=a.故选C.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 抛物线
抛物线
 是C1的任意两条互相垂直的切线,并设
是C1的任意两条互相垂直的切线,并设 ,证明
,证明 :点M的纵坐标为定值;
:点M的纵坐标为定值;
 的焦点
的焦点 为焦点.
为焦点.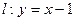 上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;
上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;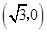 ,一条渐近线m:
,一条渐近线m: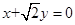 ,设过点A
,设过点A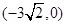 的直线l的方向向量
的直线l的方向向量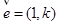 。
。 ,且a与l的距离为
,且a与l的距离为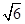 ,求K的值;
,求K的值;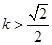 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为 的直线
的直线 过椭圆
过椭圆 的右焦点,则
的右焦点,则



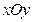 中,动点P到两定点
中,动点P到两定点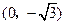 ,
,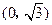 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为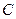 ,过点
,过点 ⊥x轴于点C,
⊥x轴于点C,  ,
, ,动点
,动点 到直线
到直线
 交点
交点 两点(
两点(
 满足
满足 ,求直线
,求直线 的斜率的取值范围
的斜率的取值范围
 、
、 满足
满足 则
则 的最大值为( )
的最大值为( ) 之间的“直角距离”为
之间的“直角距离”为 。若
。若 到点
到点 的“直角距离”相等,其中实数
的“直角距离”相等,其中实数 满足
满足 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长度之和为
的轨迹的长度之和为