题目内容
如图,在直角坐标系中,O为坐标原点,直线 ⊥x轴于点C,
⊥x轴于点C,  ,
, ,动点
,动点 到直线
到直线 的距离是它到点D的距离的2倍
的距离是它到点D的距离的2倍
(I)求点 的轨迹方程;
的轨迹方程;
(II)设点K为点 的轨迹与x轴正半轴的交点,直线
的轨迹与x轴正半轴的交点,直线 交点
交点 的轨迹于
的轨迹于 两点(
两点( 与点K均不重合),且满足
与点K均不重合),且满足
 求直线EF在X轴上的截距;
求直线EF在X轴上的截距;
(Ⅲ)在(II)的条件下,动点 满足
满足 ,求直线
,求直线 的斜率的取值范围
的斜率的取值范围

 ⊥x轴于点C,
⊥x轴于点C,  ,
, ,动点
,动点 到直线
到直线 的距离是它到点D的距离的2倍
的距离是它到点D的距离的2倍
(I)求点
 的轨迹方程;
的轨迹方程;(II)设点K为点
 的轨迹与x轴正半轴的交点,直线
的轨迹与x轴正半轴的交点,直线 交点
交点 的轨迹于
的轨迹于 两点(
两点( 与点K均不重合),且满足
与点K均不重合),且满足
 求直线EF在X轴上的截距;
求直线EF在X轴上的截距;(Ⅲ)在(II)的条件下,动点
 满足
满足 ,求直线
,求直线 的斜率的取值范围
的斜率的取值范围

(Ⅰ)动点M的轨迹方程为: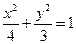 ;(Ⅱ)直线EF在X轴上的截距为
;(Ⅱ)直线EF在X轴上的截距为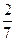 ;(Ⅲ)
;(Ⅲ)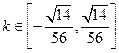 。
。
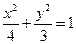 ;(Ⅱ)直线EF在X轴上的截距为
;(Ⅱ)直线EF在X轴上的截距为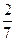 ;(Ⅲ)
;(Ⅲ)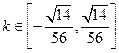 。
。(I)依题意知,点 的轨迹是以点
的轨迹是以点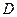 为焦点、直线
为焦点、直线 为其相应准线,
为其相应准线,
离心率为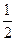 的椭圆
的椭圆
设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又 ,
,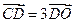 ,∴点
,∴点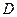 在x轴上,且
在x轴上,且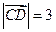 ,则
,则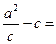 3,
3,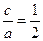
解之得: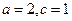 ,
,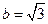

∴坐标原点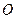 为椭圆的对称中心
为椭圆的对称中心
∴动点M的轨迹方程为: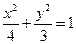

(II)设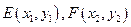 ,设直线
,设直线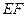 的方程为
的方程为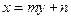 (-2〈n〈2),代入
(-2〈n〈2),代入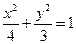 得
得
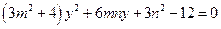

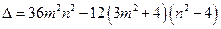 ,
,

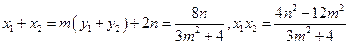
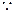
 ,K(2,0),
,K(2,0),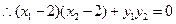 ,
,
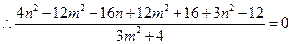 ,
,
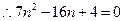

解得: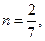
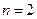 (舍)
(舍) ∴ 直线EF在X轴上的截距为
∴ 直线EF在X轴上的截距为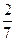
(Ⅲ)设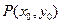 ,由
,由 知,
知,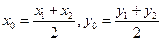

直线 的斜率为
的斜率为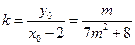

当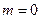 时,
时,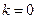 ;
;
当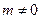 时,
时,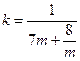 ,
,
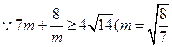 时取“=”)或
时取“=”)或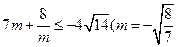 时取“=”),
时取“=”),
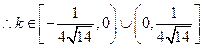
综上所述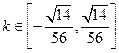
 的轨迹是以点
的轨迹是以点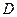 为焦点、直线
为焦点、直线 为其相应准线,
为其相应准线,离心率为
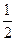 的椭圆
的椭圆设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又
 ,
,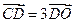 ,∴点
,∴点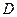 在x轴上,且
在x轴上,且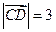 ,则
,则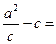 3,
3,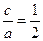
解之得:
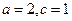 ,
,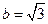

∴坐标原点
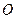 为椭圆的对称中心
为椭圆的对称中心
∴动点M的轨迹方程为:
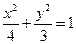

(II)设
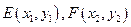 ,设直线
,设直线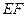 的方程为
的方程为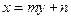 (-2〈n〈2),代入
(-2〈n〈2),代入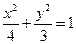 得
得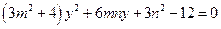

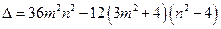 ,
,

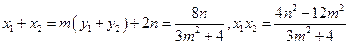
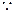
 ,K(2,0),
,K(2,0),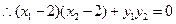 ,
,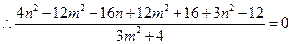 ,
,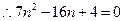

解得:
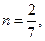
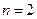 (舍)
(舍) ∴ 直线EF在X轴上的截距为
∴ 直线EF在X轴上的截距为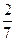
(Ⅲ)设
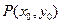 ,由
,由 知,
知,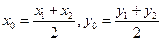

直线
 的斜率为
的斜率为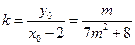

当
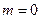 时,
时,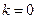 ;
;当
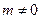 时,
时,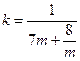 ,
,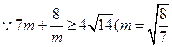 时取“=”)或
时取“=”)或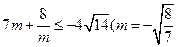 时取“=”),
时取“=”),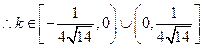
综上所述
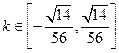

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
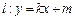 (其中
(其中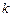 ,
, 为整数)与椭圆
为整数)与椭圆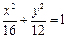 交于不同两点
交于不同两点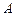 ,
,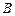 ,与双曲线
,与双曲线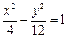 交于不同两点
交于不同两点 ,
, ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量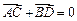 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. ,O为原点,F为右焦点,点M是椭圆右准线
,O为原点,F为右焦点,点M是椭圆右准线 上(除去与
上(除去与 轴的交点)的动点,过F作OM的垂线与以OM为直线的圆交于点N,则线段ON的长为 ( )
轴的交点)的动点,过F作OM的垂线与以OM为直线的圆交于点N,则线段ON的长为 ( )


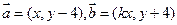 (
(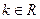 ),
),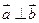 ,动点
,动点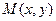 的轨迹为T.
的轨迹为T.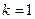 时,已知
时,已知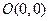 、
、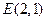 ,试探究是否存在这样的点
,试探究是否存在这样的点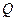 :
: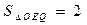 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由. 图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为.
图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为.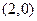 ,动点
,动点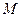 在双曲线
在双曲线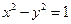 上运动,且
上运动,且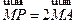 ,求点P的轨迹方程.
,求点P的轨迹方程.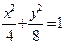 ,过原点且倾斜角为
,过原点且倾斜角为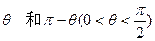 的两条直线分别交椭圆于A、C和B、D两点.(1)用
的两条直线分别交椭圆于A、C和B、D两点.(1)用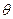 表示四边形ABCD的面积S;(2)当
表示四边形ABCD的面积S;(2)当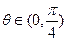 时,求S的最大值.
时,求S的最大值.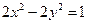 共焦点,且过(
共焦点,且过(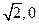 )
)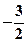 ,
,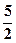 )在椭圆上.
)在椭圆上. 短轴的3倍,且过点A(4,0).
短轴的3倍,且过点A(4,0).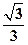 x.
x.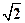 ,且过点(4,
,且过点(4,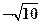 ).
).