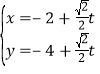题目内容
【题目】已如椭圆C:![]() 的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
(1)求椭圆C的标准方程;
(2)设动直线l交椭圆C于P,Q两点,直线OP,OQ的斜率分别为k,k'.若![]() ,求证△OPQ的面积为定值,并求此定值.
,求证△OPQ的面积为定值,并求此定值.
【答案】(1)![]() ;(2)△OPQ的面积为定值,且此定值为
;(2)△OPQ的面积为定值,且此定值为![]() ,见解析
,见解析
【解析】
(1)根据等腰直角三角形可知,![]() ,根据
,根据![]() 求解椭圆方程;(2)当
求解椭圆方程;(2)当![]() 与
与![]() 轴垂直时,设
轴垂直时,设![]() ,代入
,代入![]() 和椭圆方程,得到面积,当
和椭圆方程,得到面积,当![]() 与
与![]() 轴不垂直时,设直线l的方程为
轴不垂直时,设直线l的方程为![]() ,联立方程,得到根与系数的关系,并表示面积,得到面积是定值.
,联立方程,得到根与系数的关系,并表示面积,得到面积是定值.
(1)设椭圆C的左、右焦点分别为F1,F2.依题查,有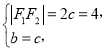 得
得![]() ,则
,则![]() ,
,
所以椭圆C的标准方程为![]() .
.
(2)证明:①当直线1与x轴垂直时,设直线l的方程为![]() ,
,![]() ,
,![]() .
.
由![]() ,且
,且![]() ,解得
,解得![]() ,
,![]() 或
或![]() ,
,![]() ,所以
,所以![]() .
.
②当直线l与x轴不垂直时,设直线l的方程为![]() ,
,![]() ,
,![]() .
.
联立直线l和椭圆C的方程,得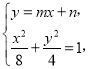 整理得
整理得![]() .
.
![]() ,
,![]() ,
,![]() .
.
由![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() ,整理得
,整理得![]() ,则
,则![]() .
.
又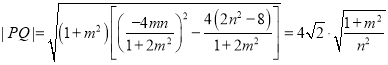 ,
,
点O到直线PQ的距离为![]() ,所以
,所以![]() .
.
综上,△OPQ的面积为定值,且此定值为![]() .
.

练习册系列答案
相关题目
【题目】某城市自2014年至2019年每年年初统计得到的人口数量如表所示.
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:万) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)设第![]() 年的人口数量为
年的人口数量为![]() (2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2014年为第1年),根据表中的数据,描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势;
(2)研究统计人员用函数![]() 拟合该城市的人口数量,其中
拟合该城市的人口数量,其中![]() 的单位是年.假设2014年初对应
的单位是年.假设2014年初对应![]() ,
,![]() 的单位是万.设
的单位是万.设![]() 的反函数为
的反函数为![]() ,求
,求![]() 的值(精确到0.1),并解释其实际意义.
的值(精确到0.1),并解释其实际意义.