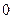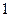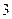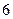题目内容
(本小题满分12分)已知函数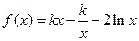 ,
,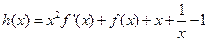 .
.
(I)证明:当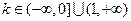 时,函数
时,函数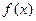 在其定义域内为单调函数;(II)若函数
在其定义域内为单调函数;(II)若函数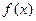 的图象在点(1,
的图象在点(1,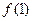 )处的切线斜率为0,且当
)处的切线斜率为0,且当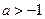 时,
时,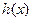 ≥
≥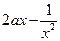 在
在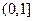 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
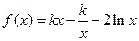 ,
,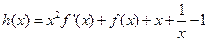 .
.(I)证明:当
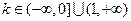 时,函数
时,函数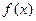 在其定义域内为单调函数;(II)若函数
在其定义域内为单调函数;(II)若函数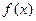 的图象在点(1,
的图象在点(1,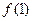 )处的切线斜率为0,且当
)处的切线斜率为0,且当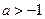 时,
时,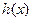 ≥
≥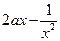 在
在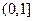 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.(II) 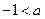 ≤1
≤1
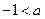 ≤1
≤1(I) 易知f(x)的定义域为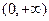 ,
,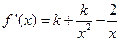 .当k=0时,
.当k=0时, 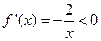 ,故f(x)在
,故f(x)在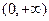 内单调递减;当k∈
内单调递减;当k∈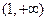 时,
时, 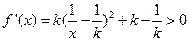 ,故f(x)在
,故f(x)在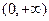 内单调递增;当k∈
内单调递增;当k∈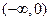 时,令
时,令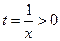 ,则
,则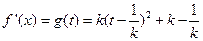 ,其对称轴
,其对称轴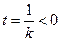 , ∴
, ∴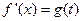 在
在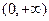 内单调递减,则
内单调递减,则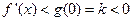 ,故f(x)在
,故f(x)在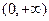 内单调递减.综上所述, 当
内单调递减.综上所述, 当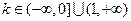 时, 函数
时, 函数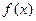 在其定义域内为单调函数.
在其定义域内为单调函数.
(II)由题意知,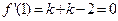 ,∴k=1,故
,∴k=1,故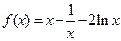 ,
, 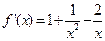 ,∴
,∴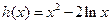 ,
, 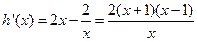 .易知x∈(0,1)时,
.易知x∈(0,1)时, 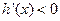 , ∴h(x)在
, ∴h(x)在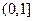 上有最小值h(1)=1.令
上有最小值h(1)=1.令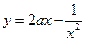 ,则
,则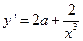 ,由
,由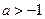 ,∴
,∴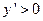 在
在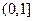 上恒成立,即
上恒成立,即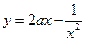 在
在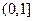 上单调递增, 其最大值为
上单调递增, 其最大值为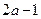 .依题意得:1≥
.依题意得:1≥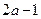 , ∴
, ∴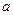 ≤1. 又
≤1. 又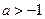 , 故
, 故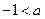 ≤1.
≤1.
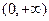 ,
,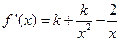 .当k=0时,
.当k=0时, 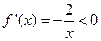 ,故f(x)在
,故f(x)在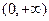 内单调递减;当k∈
内单调递减;当k∈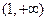 时,
时, 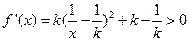 ,故f(x)在
,故f(x)在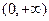 内单调递增;当k∈
内单调递增;当k∈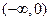 时,令
时,令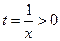 ,则
,则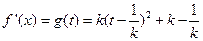 ,其对称轴
,其对称轴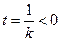 , ∴
, ∴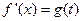 在
在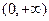 内单调递减,则
内单调递减,则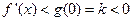 ,故f(x)在
,故f(x)在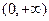 内单调递减.综上所述, 当
内单调递减.综上所述, 当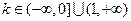 时, 函数
时, 函数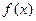 在其定义域内为单调函数.
在其定义域内为单调函数.(II)由题意知,
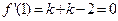 ,∴k=1,故
,∴k=1,故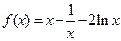 ,
, 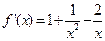 ,∴
,∴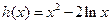 ,
, 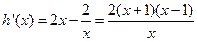 .易知x∈(0,1)时,
.易知x∈(0,1)时, 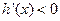 , ∴h(x)在
, ∴h(x)在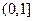 上有最小值h(1)=1.令
上有最小值h(1)=1.令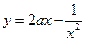 ,则
,则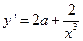 ,由
,由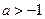 ,∴
,∴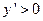 在
在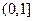 上恒成立,即
上恒成立,即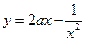 在
在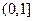 上单调递增, 其最大值为
上单调递增, 其最大值为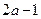 .依题意得:1≥
.依题意得:1≥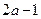 , ∴
, ∴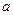 ≤1. 又
≤1. 又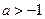 , 故
, 故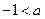 ≤1.
≤1. 
练习册系列答案
相关题目
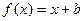 的图像与函数
的图像与函数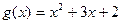 的图象相切,记
的图象相切,记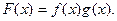
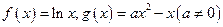 .
.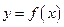 与
与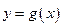 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数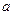 的值并求点P的坐标;(2)若函数
的值并求点P的坐标;(2)若函数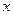 轴的垂线分别与
轴的垂线分别与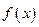 的图像和
的图像和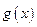 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作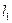 ,以T为切点作
,以T为切点作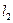 .是否存在实数
.是否存在实数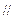
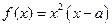 .
.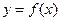 在点
在点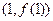 处的切线
处的切线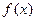 在区间[0,2]上的最大值。
在区间[0,2]上的最大值。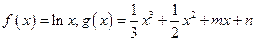 ,直线
,直线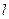 与函数
与函数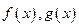 的图象都相切于点
的图象都相切于点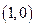 。
。 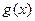 的解析式;
的解析式;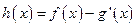 (其中
(其中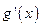 是
是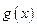 的导函数),求函数
的导函数),求函数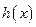 的极大值.
的极大值.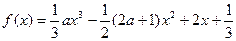 ,
,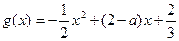
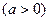 (Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,
(Ⅰ)求f (x)的单调递增区间;(Ⅱ)若在区间[0,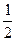 ]内至少存在一实数
]内至少存在一实数 x0使得
x0使得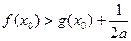 成立,求实数a的取值范围.
成立,求实数a的取值范围.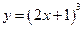 在
在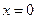 处的导数( )
处的导数( )