��Ŀ����
���ϰ˹�ɽij�ֶ���ʳƷ�Ǿ���A��B��C��������ӹ����ɵģ�A��B��C����IJ�Ʒ�ϸ��ʷֱ�Ϊ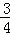 ��
��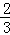 ��
��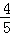 ����֪ÿ������ļӹ������������������ӹ��IJ�Ʒ��Ϊ�ϸ�ʱ��ƷΪһ��Ʒ�������κϸ�Ϊ����Ʒ��������Ϊ��Ʒ���������г���
����֪ÿ������ļӹ������������������ӹ��IJ�Ʒ��Ϊ�ϸ�ʱ��ƷΪһ��Ʒ�������κϸ�Ϊ����Ʒ��������Ϊ��Ʒ���������г���
������ʽ����ǰ��������2��ʳƷ������2��ʳƷ��Ϊ��Ʒ�ĸ��ʣ�
�������Ϊ�ӹ������в�Ʒ�ϸ�Ĵ�������εķֲ��к���ѧ������
(I)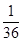 ;(II)
;(II)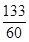 .
.
����������������� �����2��ʳƷ�����������ϸ�ĸ���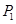 ������һ��ʳƷ���������ϸ���һ�����������ϸ�ĸ���
������һ��ʳƷ���������ϸ���һ�����������ϸ�ĸ���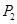 �������������������ϸ�ĸ���
�������������������ϸ�ĸ���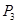 ��������ĸ���Ϊ
��������ĸ���Ϊ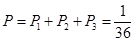 ;����������ɵ�
;����������ɵ�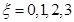 �������ɢ�����������ȡÿ��ֵ�ĸ��ʣ�����
�������ɢ�����������ȡÿ��ֵ�ĸ��ʣ�����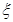 �ķֲ��У��ɷֲ������������
�ķֲ��У��ɷֲ������������
���������(I) 2��ʳƷ��Ϊ��Ʒ�����Ϊ��
��2��ʳƷ�����������ϸ� ��
��
����һ��ʳƷ���������ϸ���һ�����������ϸ�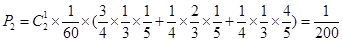 ;
;
�����������������ϸ�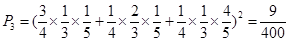 ;
;
����2��ʳƷ��Ϊ��Ʒ�ĸ���Ϊ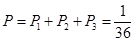 ;
;
����������ɵ�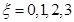 ��
��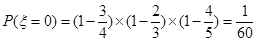 ��
��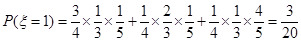 ��
��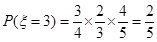 ��
��
��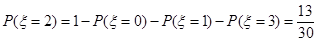 P����=2��=1��P����=0����P����=1����P����=3��=
P����=2��=1��P����=0����P����=1����P����=3��=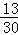 ���õ��εķֲ������£�
���õ��εķֲ������£�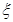
0 1 2 3 
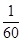
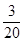
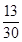
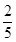
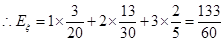
���㣺1.������¼��ĸ��ʳ˷���ʽ��2.��ɢ�������������ֲ��У�3.��ɢ����������������뷽�

�������ṩ��ij�ؽ������·ݣ�30�죩����������µ�ͳ�Ʊ����£�
| ���������t (�����) | t 22�� 22�� | 22��<t 28�� 28�� | 28��<t 32�� 32�� | 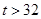 �� �� |
| ���� | 6 | 12 | 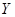 | 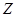 |
ijˮ���̸��ݶ�������۾��飬���·ݵ����������t (��λ����)�����ϵ�����Ӱ�����±���
| ���������t (�����) | t 22�� 22�� | 22��<t 28�� 28�� | 28��<t 32�� 32�� | 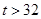 �� �� |
�����۶�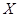 ��ǧԪ�� ��ǧԪ�� | 2 | 5 | 6 | 8 |
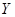 ��
�� 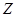 ��ֵ��
��ֵ��(��) ����Ƶ��Ϊ���ʣ������·����������۶�������ͷ��
(��) ����������²�����32��ʱ���������۶����5ǧԪ�ĸ��ʣ�
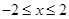 ��
��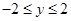 ����
���� ������Ϊ
������Ϊ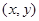 .
.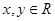 ʱ����
ʱ����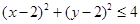 �ĸ��ʣ�
�ĸ��ʣ�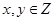 ʱ����
ʱ����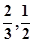 ��ÿ�����Ƿ����Ӱ�죬�����Ե�5�����У�
��ÿ�����Ƿ����Ӱ�죬�����Ե�5�����У�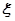 �ķֲ���������.
�ķֲ���������.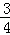 ��
�� ��
��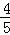 ����֪ÿ������ļӹ������������������ӹ��IJ�Ʒ��Ϊ�ϸ�ʱ��ƷΪһ��Ʒ�������κϸ�Ϊ����Ʒ��������Ϊ��Ʒ���������г���
����֪ÿ������ļӹ������������������ӹ��IJ�Ʒ��Ϊ�ϸ�ʱ��ƷΪһ��Ʒ�������κϸ�Ϊ����Ʒ��������Ϊ��Ʒ���������г���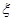 Ϊȡ����3֦��һ��Ʒ��֦������
Ϊȡ����3֦��һ��Ʒ��֦������
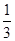 ��
��